Question

已知在△ABC中，a、b、c分别为角A、B、C的对边，设f（x）＝a²x²-（a²-b²）x-4c².

（1）若f（1）＝0，且B-C＝，求角C；

（2）若f（2）＝0，求角C的取值范围.

Answer 1

解:（1）由f（1）=0，得a²-a²+b²-4c²=0，∴b=2c.                          

又由正弦定理，得b=2RsinB，c=2RsinC，将其代入上式，得sinB=2sinC.           

∵B-C=，∴B=+C，将其代入上式，得sin（+C）=2sinC.                  

∴sincosC+cossinC=2sinC，整理得，sinC=cosC.                         

∴tanC=.                                                               

∵角C是三角形的内角，∴C=.                                             

（2）∵f（2）=0，∴4a²-2a²+2b²-4c²=0，即a²+b²-2c²=0.                         

由余弦定理，得cosC=                                          

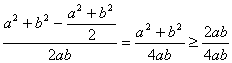==（当且仅当a=b时取等号）.           

∴cosC≥，∠C是锐角.

又∵余弦函数在（0，）上递减，∴0＜C≤.