题目内容
一个质量均匀的正四面体型的模具,其四个面上分别标有数字1,2,3,4,若连续投掷三次,取三次面向上的数字分别作为三角形的边长,则其能构成钝角三角形的概率为( )A.

B.

C.

D.

【答案】分析:连续投掷三次,每次均有四种可能,即共有43=64种情况,能构成钝角三角形所有排列情况,(4,3,2,);(4,2,3);(3,4,2);(3,2,4);(2,4,3);(2,3,4);(3,2,2),(2,3,2),(2,2,3)共9种情况,利用古典概型的概率公式求出概率.
解答:解:∵其四个面上分别标有数字1,2,3,4,连续投掷三次,每次均有四种可能
∴共有43=64种情况,
而能构成钝角三角形的情况为4,3,2,与3,2,2的所有排列情况,
即(4,3,2,);(4,2,3);(3,4,2);(3,2,4);(2,4,3);(2,3,4);(3,2,2),(2,3,2),(2,2,3)共9种情况
∴构成钝角三角形的概率为: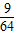
故选C.
点评:本题考查了等可能事件的概率,关键利用排列组合的知识算出方法数,另外若问题从正面考虑比较麻烦,可以从它的对立事件来考虑.
解答:解:∵其四个面上分别标有数字1,2,3,4,连续投掷三次,每次均有四种可能
∴共有43=64种情况,
而能构成钝角三角形的情况为4,3,2,与3,2,2的所有排列情况,
即(4,3,2,);(4,2,3);(3,4,2);(3,2,4);(2,4,3);(2,3,4);(3,2,2),(2,3,2),(2,2,3)共9种情况
∴构成钝角三角形的概率为:
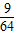
故选C.
点评:本题考查了等可能事件的概率,关键利用排列组合的知识算出方法数,另外若问题从正面考虑比较麻烦,可以从它的对立事件来考虑.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个质量均匀的正四面体型的模具,其四个面上分别标有数字1,2,3,4,若连续投掷三次,取三次面向上的数字分别作为三角形的边长,则其能构成钝角三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 B.
B. C.
C. D.
D.