题目内容
 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:BC1∥平面ACD1;
(2)证明:A1D⊥D1E;
(3)当E为AB的中点时,求四棱锥E-ACD1的体积.
解:(1)证明:∵ABCD-A1B1C1D1是长方体,∴AB∥D1C1,AB=D1C1,
∴AB C1 D1为平行四边形,∴B C1∥AD1,
又∵BC1?平面ACD1,AD1?平面ACD1,
∴BC1∥平面ACD1.
(2)证明:∵AE⊥平面AA1D1D,A1D?平面AA1D1D,
∴A1D⊥AE.
∵四边形AA1D1D为正方形,∴A1D⊥A D1,
又AD1∩AE=A,∴A1D⊥平面AD1E,
∵D1E?平面AD1E,∴A1D⊥D1E.
(3)解:∵S△ACE= =
= =
= .
.
∴ =
= =
=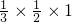 =
= .
.
所以三棱锥E-ACD1的体积 .
.
分析:(1)利用线面平行的判定定理即可证明;
(2)利用线面垂直的性质定理和判定定理即可证明;
(3)利用 =
= 即可求出.
即可求出.
点评:熟练掌握线面平行的判定定理、线面垂直的判定定理和性质定理及等积变形是解题的关键.
∴AB C1 D1为平行四边形,∴B C1∥AD1,
又∵BC1?平面ACD1,AD1?平面ACD1,
∴BC1∥平面ACD1.
(2)证明:∵AE⊥平面AA1D1D,A1D?平面AA1D1D,
∴A1D⊥AE.
∵四边形AA1D1D为正方形,∴A1D⊥A D1,
又AD1∩AE=A,∴A1D⊥平面AD1E,
∵D1E?平面AD1E,∴A1D⊥D1E.
(3)解:∵S△ACE=
 =
= =
= .
.∴
 =
= =
=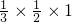 =
= .
.所以三棱锥E-ACD1的体积
 .
.分析:(1)利用线面平行的判定定理即可证明;
(2)利用线面垂直的性质定理和判定定理即可证明;
(3)利用
 =
= 即可求出.
即可求出.点评:熟练掌握线面平行的判定定理、线面垂直的判定定理和性质定理及等积变形是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.