题目内容
（2010•通州区一模）在△ABC中，若∠B=120°，AB=1，BC=2，则AC=
．
| 7 |
| 7 |
分析：设AB=c，BC=a，AC=b，由a，c及cosB的值，利用余弦定理列出关于b的方程，求出方程的解得到b的值，即为AC的长．
解答：解：∵∠B=120°，c=AB=1，a=BC=2，
∴根据余弦定理得：b2=a2+c2-2ac•cosB=4+1+2=7，
则AC=b=
．
故答案为：
∴根据余弦定理得：b2=a2+c2-2ac•cosB=4+1+2=7，
则AC=b=
| 7 |
故答案为：
| 7 |
点评：此题考查了余弦定理，以及特殊角的三角函数值，余弦定理很好的建立了三角形的边角关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
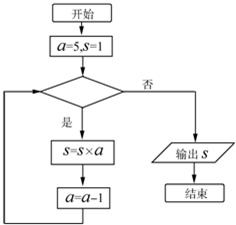（2010•通州区一模）执行图所示的程序，输出的结果为20，则判断框中应填入的条件为（ ）
（2010•通州区一模）设不等式组