题目内容
设x,y满足约束条件 ,若目标函数z=
,若目标函数z= 的最大值为10,则5a+4b的最小值为
的最大值为10,则5a+4b的最小值为
- A.

- B.

- C.10
- D.8
D
分析:画出可行域,将目标函数变形,数形结合求出目标函数的最大值,得到a,b的关系,两式相乘凑成利用基本不等式的条件,利用基本不等式求最值.
解答: 解:画出
解:画出 的可行域
的可行域
将z=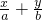 直线在y轴上的截距
直线在y轴上的截距
∵a>0,b>0,则当截距越大,z也越大,结合图象可知将其平移至点A时纵截距最大,z最大
由 可得A(4,5)
可得A(4,5)
将A(4,5)代入z=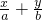 得到z最大值
得到z最大值 =10
=10
∴5a+4b= •(5a+4b)=
•(5a+4b)= ×(40+
×(40+ )
)
≥ ×(40+2
×(40+2 )=8
)=8
当且仅当 ,又
,又 =10
=10
即a= ,b=1时取等号
,b=1时取等号
故选D.
点评:本题考查线性规划问题、画出可行域、利用目标函数的几何意义、数形结合求最值、利用基本不等式求最值.
分析:画出可行域,将目标函数变形,数形结合求出目标函数的最大值,得到a,b的关系,两式相乘凑成利用基本不等式的条件,利用基本不等式求最值.
解答:
 解:画出
解:画出 的可行域
的可行域将z=
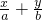 直线在y轴上的截距
直线在y轴上的截距∵a>0,b>0,则当截距越大,z也越大,结合图象可知将其平移至点A时纵截距最大,z最大
由
 可得A(4,5)
可得A(4,5)将A(4,5)代入z=
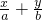 得到z最大值
得到z最大值 =10
=10∴5a+4b=
 •(5a+4b)=
•(5a+4b)= ×(40+
×(40+ )
)≥
 ×(40+2
×(40+2 )=8
)=8当且仅当
 ,又
,又 =10
=10即a=
 ,b=1时取等号
,b=1时取等号故选D.
点评:本题考查线性规划问题、画出可行域、利用目标函数的几何意义、数形结合求最值、利用基本不等式求最值.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目