题目内容
(本小题满分12分)
已知函数
(Ⅰ)判断函数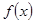 的奇偶性;
的奇偶性;
(Ⅱ)证明:函数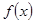 在区间
在区间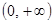 上为增函数.
上为增函数.
【答案】
⑴ 为偶函数.⑵见解析.
为偶函数.⑵见解析.
【解析】本试题主要是考查了函数的奇偶性和单调性的综合运用
(1)先判定定义域是否关于原点对称,然后求解f(-x)与f(x)的关系式得到结论。
(2)设出变量,然后作差,变形定号,下结论。
解:⑴ ,且
,且
 .
.
故 为偶函数.
为偶函数.
⑵设 ,则
,则


∴函数 在区间
在区间 上为增函数.
上为增函数.
(21)【题文】(本小题满分12分)
对于每个实数 ,设
,设 取
取 三个函数中的最小值,用分段函数写出
三个函数中的最小值,用分段函数写出 的解析式,并求
的解析式,并求 的最大值.
的最大值.
【答案】 ,
, .
.
【解析】本试题主要是考查了分段函数的解析式的求解以及函数的最值的综合运用。
利用已知函数解析式在统一坐标系下左图,然后找到所要的函数的及诶西施,进而得到结论。
解:在统一坐标系下作出三个函数的图像,可知
 ,
, .
.

练习册系列答案
相关题目