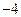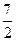题目内容
(21)(本小题10分)
(I) 为△ABC的内角,则
为△ABC的内角,则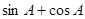 的取值范围是________ .
的取值范围是________ .
(II)给定两个长度为1的平面向量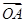 和
和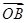 ,它们的夹角为
,它们的夹角为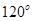 .
.
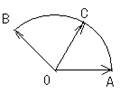
如图所示,点C在以O为圆心的圆弧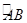 上变动
上变动
若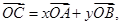 其中
其中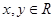 ,则
,则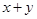 的最大值是________.
的最大值是________.

(I)
 为△ABC的内角,则
为△ABC的内角,则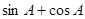 的取值范围是________ .
的取值范围是________ .(II)给定两个长度为1的平面向量
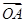 和
和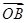 ,它们的夹角为
,它们的夹角为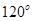 .
.如图所示,点C在以O为圆心的圆弧
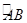 上变动
上变动若
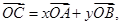 其中
其中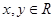 ,则
,则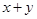 的最大值是________.
的最大值是________.1)
 ;
;(2)解 设

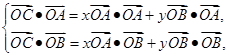 ,即
,即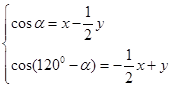 .
.∴
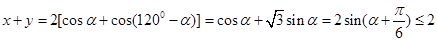
(I)根据辅助角公式,我们可以将sinA+cosA化为正弦型函数的形式,根据A为△ABC的内角,即可得到sinA+cosA的取值范围;
(II)∠AOC=α,我们可以得到x,y的解析式(含参数α),根据辅助角公式,我们可以得到x+y的表达式,然后根据三角函数的性质,即可得到x+y的最大值.
解答:解:(I)∵sinA+cosA=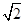 sin(A+
sin(A+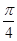 )
)
又∵A∈(0,π)
∴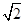 sin(A+
sin(A+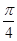 )∈(-1,
)∈(-1,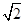 ];
];
(II)设∠AOC=α
∴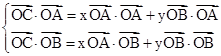
即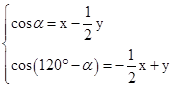
∴x+y=2[cosα+cos(120°-α)]=cosα+ sinα=2sin(x+
sinα=2sin(x+ )≤2
)≤2
故x+y的最大值是 2
故答案为:(-1,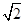 ],2
],2
(II)∠AOC=α,我们可以得到x,y的解析式(含参数α),根据辅助角公式,我们可以得到x+y的表达式,然后根据三角函数的性质,即可得到x+y的最大值.
解答:解:(I)∵sinA+cosA=
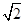 sin(A+
sin(A+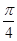 )
)又∵A∈(0,π)
∴
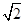 sin(A+
sin(A+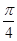 )∈(-1,
)∈(-1,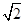 ];
];(II)设∠AOC=α
∴
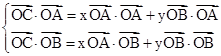
即
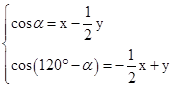
∴x+y=2[cosα+cos(120°-α)]=cosα+
 sinα=2sin(x+
sinα=2sin(x+ )≤2
)≤2故x+y的最大值是 2
故答案为:(-1,
 ],2
],2
练习册系列答案
相关题目
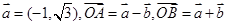 ,若
,若 是以点O为直角顶点的等腰直角三角形,则
是以点O为直角顶点的等腰直角三角形,则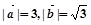 ,且
,且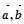 的夹角为
的夹角为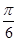 ,则|
,则|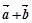 |等于( )
|等于( ) 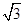
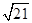
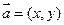 ,
,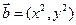 ,
,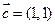 ,
,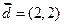 ,且
,且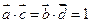 ,则起点在原点的向量
,则起点在原点的向量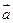 的个数为 .
的个数为 . ,
,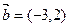 ,当
,当 为何值时,
为何值时,
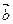 与
与
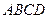 中,
中,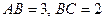 ,
,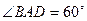 ,
, 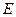 为
为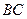 边上的中点,
边上的中点,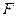 为平行四边形内(包括边界)一动点,则
为平行四边形内(包括边界)一动点,则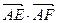 的最大值为 ▲ .
的最大值为 ▲ .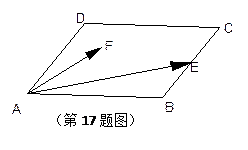
 满足关系
满足关系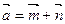 ,
,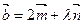 ,且
,且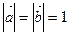 ,
, .
.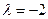 时,求
时,求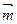 与
与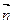 的夹角的余弦值.
的夹角的余弦值. 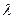 为何值时,
为何值时,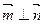 .
.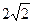 ,|q|=3,p、q的夹角为45
,|q|=3,p、q的夹角为45 °,则以a=5p+2q,b=p-3q为邻边的平行四边形过a、b起点的对角线长为 ( )
°,则以a=5p+2q,b=p-3q为邻边的平行四边形过a、b起点的对角线长为 ( )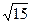 C.15 D
C.15 D .16
.16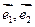 是夹角为
是夹角为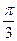 的单位向量,且
的单位向量,且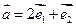 ,
,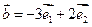 ,则
,则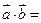 ( )
( )