题目内容
设数列{an}的前n项和为Sn,点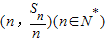 均在函数y=-x+12的图象上.
均在函数y=-x+12的图象上.(Ⅰ)写出Sn关于n的函数表达式;
(Ⅱ)求证:数列{an}是等差数列;
(Ⅲ)求数列{|an|}的前n项的和.
【答案】分析:(I)根据点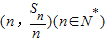 均在函数y=-x+12的图象上,则点的坐标适合方程,代入方程即可求出Sn关于n的函数表达式;
均在函数y=-x+12的图象上,则点的坐标适合方程,代入方程即可求出Sn关于n的函数表达式;
(II)当n≥2时,根据an=Sn-Sn-1求出通项,验证首项即可;
(III)由(Ⅱ)知,a1,a2,…a6>0,数列{an}从第7项起均为负数,然后讨论n与6的大小,利用分段函数表示数列{|an|}的前n项的和.
解答:解 (Ⅰ)由题设得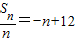 ,即Sn=n(-n+12)=-n2+12n.
,即Sn=n(-n+12)=-n2+12n.
(Ⅱ)当n=1时,an=a1=S1=11;
当n≥2时,an=Sn-Sn-1=(-n2+12n)-(-(n-1)2+12(n-1))=-2n+13;
由于此时-2×1+13=11=a1,从而数列{an}的通项公式是an=-2n+13.
(Ⅲ)由(Ⅱ)知,a1,a2,…a6>0,数列{an}从第7项起均为负数.设数列{|an|}的前n项的和为Tn.
当n≤6时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=-n2+12n;
当n≥7时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+a6-a7-…-an
=(a1+a2+…+a6)-(a7+…+an)
=2(a1+a2+…+a6)-(a1+a2+…+a6+a7+…+an)
=2S6-Sn=n2-12n+72.
所以数列{|an|}的前n项的和为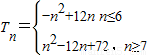 .
.
点评:本题主要考查了数列与函数的综合运用,以及等差数列的通项公式和求出,属于中档题.
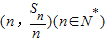 均在函数y=-x+12的图象上,则点的坐标适合方程,代入方程即可求出Sn关于n的函数表达式;
均在函数y=-x+12的图象上,则点的坐标适合方程,代入方程即可求出Sn关于n的函数表达式;(II)当n≥2时,根据an=Sn-Sn-1求出通项,验证首项即可;
(III)由(Ⅱ)知,a1,a2,…a6>0,数列{an}从第7项起均为负数,然后讨论n与6的大小,利用分段函数表示数列{|an|}的前n项的和.
解答:解 (Ⅰ)由题设得
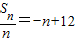 ,即Sn=n(-n+12)=-n2+12n.
,即Sn=n(-n+12)=-n2+12n.(Ⅱ)当n=1时,an=a1=S1=11;
当n≥2时,an=Sn-Sn-1=(-n2+12n)-(-(n-1)2+12(n-1))=-2n+13;
由于此时-2×1+13=11=a1,从而数列{an}的通项公式是an=-2n+13.
(Ⅲ)由(Ⅱ)知,a1,a2,…a6>0,数列{an}从第7项起均为负数.设数列{|an|}的前n项的和为Tn.
当n≤6时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=-n2+12n;
当n≥7时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+a6-a7-…-an
=(a1+a2+…+a6)-(a7+…+an)
=2(a1+a2+…+a6)-(a1+a2+…+a6+a7+…+an)
=2S6-Sn=n2-12n+72.
所以数列{|an|}的前n项的和为
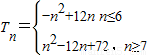 .
.点评:本题主要考查了数列与函数的综合运用,以及等差数列的通项公式和求出,属于中档题.

练习册系列答案
相关题目