题目内容
 如图,函数f(x)=sin(ωx+φ)(ω>0,|φ|<
如图,函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
分析:由题意可得f(0)=sinφ=
,再由|φ|<
可得φ 的值.再由f(
)=sin(ω•
+
)=0,ω>0,可得ω 的值,可得函数f(x)的解析式.
再根据y=Asin(ωx+φ)的图象变换规律可得结论.
| 1 |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
再根据y=Asin(ωx+φ)的图象变换规律可得结论.
解答:解:由题意可得f(0)=sinφ=
,再由|φ|<
可得φ=
.
再由f(
)=sin(ω•
+
)=0,ω>0,可得ω=
,故函数f(x)=sin(
x+
)=sin
(x+
),
故将y=f(x)的图象向右平移
个单位,可得奇函数y=sin
x的图象,
故选C.
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
再由f(
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 5 |
| 2 |
| 5 |
| 2 |
| π |
| 6 |
| 5 |
| 2 |
| π |
| 15 |
故将y=f(x)的图象向右平移
| π |
| 15 |
| 5 |
| 2 |
故选C.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
相关题目
如图,函数f(x)的图象是曲线OAB,则f(
)的值等于( )
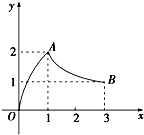
| 1 |
| f(3) |

| A、1 | B、2 | C、3 | D、0 |
 如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( ) 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象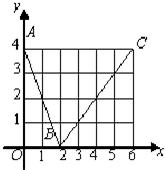 如图,函数f(x)的图象是折线段ABC,其中点A、B、C的坐标分别为(0,4),(2,0),(6,4),若f(x)的值域为[0,4],定义域为[m,n],则|m-n|的最小值为
如图,函数f(x)的图象是折线段ABC,其中点A、B、C的坐标分别为(0,4),(2,0),(6,4),若f(x)的值域为[0,4],定义域为[m,n],则|m-n|的最小值为