题目内容
【题目】如图，在直二面角D﹣AB﹣E中，四边形ABCD是边长为2的正方形，AE=EB，点F在CE上，且BF⊥平面ACE；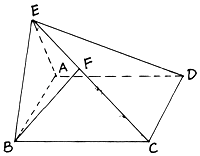 
（1）求证：AE⊥平面BCE；
（2）求二面角B﹣AC﹣E的正弦值；
（3）求点D到平面ACE的距离．
【答案】
（1）证明：∵BF⊥平面ACE，∴BF⊥AE，
∵二面角D﹣AB﹣E为直二面角，
∴平面ABCD⊥平面ABE，
又BC⊥AB，∴BC⊥平面ABE，则BC⊥AE，
又BF平面BCE，BF∩BC=B，
∴AE⊥平面BCE
（2）法一、解：连接AC、BD交于G，连接FG，
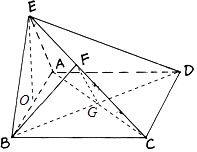
∵ABCD为正方形，∴BD⊥AC，
∵BF⊥平面ACE，BG⊥AC，∴AC⊥平面BFG，
∴FG⊥AC，即∠FGB为二面角B﹣AC﹣E的平面角，
由（1）可知，AE⊥平面BCE，∴AE⊥EB，
又AE=EB，AB=2，AE=BE= 
，
在直角三角形BCE中，CE= 
= 
，BF= 
= 
，
在正方形中，BG= ，在直角三角形BFG中，sin∠FGB= 
；
法二、以线段AB的中点为原点O，OE所在直线为x轴，AB所在直线为y轴，
过O点平行于AD的直线为z轴，建立空间直角坐标系O﹣xyz，如图．
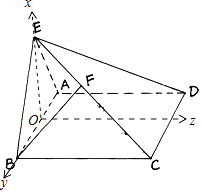
∵AE⊥面BCE，BE面BCE，∴AE⊥BE，
在Rt△AEB中，AB=2，O为AB的中点，
∴OE=1．∴A（0，﹣1，0），E（1，0，0），C（0，1，2），
=（1，1，0）， 
=（0，2，2）．
设平面AEC的一个法向量为 
=（x，y，z），
则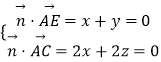 
，令x=1，得 =（1，﹣1，1）是平面AEC的一个法向量．
又平面BAC的一个法向量为 
=（1，0，0），
∴cos＜ 
＞= 
= 
．
∴二面角B﹣AC﹣E的正弦值为 
（3）法一、由（2）可知，在正方形ABCD中，BG=DG，D到平面ACE的距离等于B到平面ACE的距离，
BF⊥平面ACE，线段BF的长度就是点B到平面ACE的距离，即为D到平面ACE的距离所以D到平面的距离为 
．
法二、
解：∵AD∥z轴，AD=2，∴ 
=（0，0，2），
∴点D到平面ACE的距离d=| ||cos＜ 
＞= 
= 
．
【解析】（1）要证AE⊥平面BCE，只需证明AE垂直平面BCE内的两条相交直线BF、BC即可；（2）连接AC、BD交于G，连接FG，说明∠FGB为二面角B﹣AC﹣E的平面角，然后求二面角B﹣AC﹣E的大小；（3）利用VD﹣ACE=VE﹣ACD ， 求点D到平面ACE的距离，也可以利用空间直角坐标系，向量的数量积，证明垂直，求出向量的模．
