题目内容
设动直线x=a与函数f(x)=2sin2(
+x)和g(x)=
cos2x的图象分别交于M、N两点,则|MN|的最大值为( )
| π |
| 4 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
分析:利用二倍角公式先化简f(x),将|MN|表示成a的三角函数,利用公式asinx+bcosx=
sin(x+θ)化简|MN|,利用三角函数的有界性求出最大值.
| a2+b2 |
解答:解:f(x)=1-cos(
+2x)=1+sin2x,|MN|=|f(a)-g(a)|=|1+sin2a-
cos2a|
=|2sin(2a-
)+1|≤3.
故选D
| π |
| 2 |
| 3 |
=|2sin(2a-
| π |
| 3 |
故选D
点评:本题考查三角函数的二倍角公式、诱导公式、公式asinx+bcosx=
sin(x+θ)、三角函数的有界性.
| a2+b2 |

练习册系列答案
相关题目
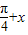 )和g(x)=
)和g(x)=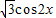 的图象分别交于M、N两点,则|MN|的最大值为 .
的图象分别交于M、N两点,则|MN|的最大值为 .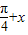 )和g(x)=
)和g(x)=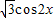 的图象分别交于M、N两点,则|MN|的最大值为 .
的图象分别交于M、N两点,则|MN|的最大值为 .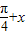 )和g(x)=
)和g(x)=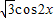 的图象分别交于M、N两点,则|MN|的最大值为 .
的图象分别交于M、N两点,则|MN|的最大值为 .