题目内容
已知函数![]() 处取得极值.
处取得极值.
(I)求b的值;
(II)若当![]() 恒成立,求c的取值范围;
恒成立,求c的取值范围;
|
解:(I)∵f(x)=x3-![]() x2+bx+c,
x2+bx+c,
∴f′(x)=3x2-x+b
∵f(x)在x=1处取得极值,
∴f′(1)=3-1+b=0. ∴b=-2
(II)f(x)=x3-![]() x2-2x+c.
x2-2x+c.
∵f′(x)=3x2-x-2=(3x+2)(x-1),
| x | (-∞,- | - | (- | 1 | (1,+ ∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) |
|
|
| - |
|
∴当![]() 时,函数f(x)单调递增;
时,函数f(x)单调递增;
当x∈(-![]() ,1)时,函数f(x)单调递减;
,1)时,函数f(x)单调递减;
当x∈(1,2![]() 时,函数f(x)单调递增.
时,函数f(x)单调递增.
∴当x=-![]() 时,f(x)有极大值
时,f(x)有极大值![]() +c
+c
又![]()
∴x∈[-1,2]时,f(x)最大值为f(2)=2+c.
∴c2>2+c.
∴c<-1或c>2
(III)对任意的![]() 恒成立.
恒成立.
由(II)可知,当x=1时,f(x)有极小值-![]() +c.
+c.
又![]()
∴x∈[-1,2]时,f(x)最小值为-![]() +c.
+c.
![]() ,故结论成立
,故结论成立

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
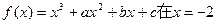 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线 在点(1,0)处相切,求a、b
在点(1,0)处相切,求a、b 、c的值.
、c的值. 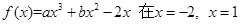 处取得极值。(1)求函数
处取得极值。(1)求函数 的解析式;
的解析式; 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线 在点(1,0)处相切,则函数
在点(1,0)处相切,则函数 的表达式为
.
的表达式为
.  处取得极值为2.
处取得极值为2. 的解析式;
的解析式; 上为增函数,求实数m的取值范围;
上为增函数,求实数m的取值范围;
 图象上的任意一点,直线l与
图象上的任意一点,直线l与 的图象相切于点P,求直线l的斜率的取值范围.
的图象相切于点P,求直线l的斜率的取值范围. 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线 在点(1,0)处相切,则函数
在点(1,0)处相切,则函数 的表达式为
.
的表达式为
.