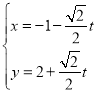题目内容
【题目】在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数,
(t为参数,![]() ).在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线
).在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的普通方程;
的普通方程;
(2)若直线l的极坐标方程为![]() ,其中
,其中![]() 满足
满足![]() ,若曲线
,若曲线![]() 和
和![]() 的公共点均在l上,求
的公共点均在l上,求![]() .
.
【答案】(1)![]() :
:![]() ,
,![]() :
:![]() ;(2)
;(2)![]()
【解析】
(1)![]() ,可得
,可得![]() ,根据
,根据![]() ,即可求得
,即可求得![]() 的普通方程,由
的普通方程,由![]() ,根据极坐标与直角坐标的互化公式:
,根据极坐标与直角坐标的互化公式: ,即可求得
,即可求得![]() 的普通方程为;
的普通方程为;
(2)由直线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() 满足
满足![]() ,得
,得![]() 的普通方程为
的普通方程为![]() ,
,![]() 的普通方程为
的普通方程为![]() 和
和![]() 的普通方程为
的普通方程为![]() ,可求得公共弦方程,即可求得
,可求得公共弦方程,即可求得![]() 的值.
的值.
(1)![]()
![]() ,
,
![]()
![]() ,
,
两式平方相加得![]() 的普通方程为
的普通方程为![]() .
.
![]()
![]()
可得![]() ,
,
故![]() 的普通方程为
的普通方程为![]() ,
,
![]()
![]() .
.
(2)由直线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() 满足
满足![]() ,
,
得![]() 的普通方程为
的普通方程为![]() ,
,
![]() 曲线
曲线![]() 和
和![]() 的公共点均在
的公共点均在![]() 上,
上,
![]()
![]() 为圆
为圆![]() 和
和![]() 的公共弦所在的直线.
的公共弦所在的直线.
![]()
![]() 的普通方程为
的普通方程为![]()
![]() ①
①
![]() 的普通方程为
的普通方程为![]()
![]() ②
②
①![]() ②得
②得![]() 即为l,
即为l,
故![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.