题目内容
函数y=2cos2x+1( )的最小正周期为( )
)的最小正周期为( )
A B
B C
C D
D
B
解析试题分析: ,所以函数的周期为
,所以函数的周期为 .
.
考点:二倍角的余弦;三角函数的周期性及其求法.
点评:此题考查了三角函数的周期性及其求法,以及二倍角的余弦函数公式,其中利用二倍角的三角函数公式将函数解析式化为一个角的余弦函数是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ( )
( )
A. | B. | C. | D. |
 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数y=sin (2x+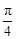 )的图象可由函数y=sin 2x的图象
)的图象可由函数y=sin 2x的图象
A.向左平移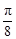 个单位长度而得到 个单位长度而得到 | B.向右平移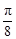 个单位长度而得到 个单位长度而得到 |
C.向左平移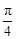 个单位长度而得到 个单位长度而得到 | D.向右平移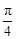 个单位长度而得到 个单位长度而得到 |
已知方程 在
在 有两个不同的解
有两个不同的解 (
( ),则下面结论正确的是:
),则下面结论正确的是:
A. | B. |
C. | D. |
使函数
 为增函数的区间是( )
为增函数的区间是( )
A. | B. | C. | D. |
已知 为第二象限角,则
为第二象限角,则 的值是 ( )
的值是 ( )
| A.3 | B.-3 | C.1 | D.-1 |
函数 的定义域是( )
的定义域是( )
A. | B. |
C. | D. |
下列关系式中正确的是( )
A. | B. |
C. | D. |