题目内容
已知函数
，若有f（b）=g（a），则a的取值范围为（ ）A．（1，3）
B．（2-
）C．[2-
]D．[2，3]
【答案】分析：设函数f（x）的值域为A，g（x）的值域为B，根据f（b）=g（a），则必有g（a）∈A∩B，从而可求出a的取值范围..
解答：解：因为f（x）=ex-2＞-2，g（x）=-x2+4x-5=-（x-2）2-1≤-1，f（b）=g（a），
所以-2＜g（a）≤-1，即-2＜-a2+4a-5≤-1，解得1＜a＜3．
故选A．
点评：本题考查二次函数的有关性质，考查利用所学知识灵活解决问题的能力．
解答：解：因为f（x）=ex-2＞-2，g（x）=-x2+4x-5=-（x-2）2-1≤-1，f（b）=g（a），
所以-2＜g（a）≤-1，即-2＜-a2+4a-5≤-1，解得1＜a＜3．
故选A．
点评：本题考查二次函数的有关性质，考查利用所学知识灵活解决问题的能力．
练习册系列答案
全能练考卷系列答案
相关题目
，若有f(a)＝g(b)，则b的取值范围为
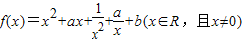．若实数a、b使得f（x）=0有实根，则a2+b2的最小值为（ ）
，若有f（b）=g（a），则a的取值范围为（ ）
）
]
，若有f（b）=g（a），则a的取值范围为（ ）
）
]