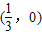题目内容
函数y=lg（3x+1）的定义域是
(-
，+∞)
| 1 |
| 3 |
(-
，+∞)
．| 1 |
| 3 |
分析：直接由对数型函数的真数大于0求解．
解答：解：由3x+1＞0，解得：x＞-
．
∴函数y=lg（3x+1）的定义域是(-
，+∞)．
故答案为：(-
，+∞)．
| 1 |
| 3 |
∴函数y=lg（3x+1）的定义域是(-
| 1 |
| 3 |
故答案为：(-
| 1 |
| 3 |
点评：本题考查了函数的定义域及其求法，是基础的计算题．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
把函数y=lg（3x）的图象按向量
平移，得到函数y=lg(x+1)的图象，则
为（ ）
| a |
| a |
| A、（-1，lg3） | ||
| B、（1，-lg3） | ||
| C、（-1，-lg3） | ||
D、(
|
) B.(
,+∞) C.(-∞,
) D.(-1,
］
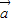平移，得到函数
为（ ）