题目内容
7．若函数f（x）=$\frac{\root{3}{3x+1}}{kx^2+3k+4}$的定义域为R．求实数k的取值范围．分析 根据函数成立的条件建立不等式关系即可．
解答 解：∵函数f（x）=$\frac{\root{3}{3x+1}}{kx^2+3k+4}$的定义域为R，
∴不等式kx2+3k+4≠0恒成立，
若k=0，则不等式等价为4≠0．满足条件，
若k≠0，则判别式△=0-4k（3k+4）＜0，
即4k（3k+4）＞0，解得k＜$-\frac{4}{3}$或k＞0，
综上得k＜$-\frac{4}{3}$或k≥0．
点评 本题主要考查函数定义域的应用，根据不等式恒成立是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．若双曲线x${\;}^{2}-\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的一条渐近线与圆x${\;}^{2}+（y-\sqrt{3}）^{2}$=1至多有一个交点，则双曲线的离心率的取值范围是（ ）
| A． | （1，2] | B． | [2，+∞） | C． | （1，$\sqrt{3}$] | D． | [$\sqrt{3}，+∞$） |
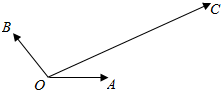如图，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°，|$\overrightarrow{OC}$|=2$\sqrt{3}$，用$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$为$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$．
17．下列函数为奇函数的是 （ ）
| A． | y=-|x| | B． | y=2-x | C． | y=$\frac{1}{{x}^{3}}$ | D． | y=-x2+8 |