题目内容
解下列函数的定义域(1)y=

(2)y=

(3)y=
 .
.
【答案】分析:(1)中根据二次根式的定义知被开方数大于等于0得到x的不等式求出解集即可;
(2)也根据二次根式的定义及分母不为零,得到x的不等式求出解集即可;
(3)根据二次根式的定义及对数函数的性质,得到x的不等式求出解集即可.
解答:解:(1)由题得:x2-2x-3≥0 解得x≥3或x≤-1,所以函数的定义域为(-∞,-1]∪[3,+∞);
(2)由题知:2x-1>解得x>0,所以函数的定义域为(0,+∞).
(3)由题知:log (2x-1)≥0,解得
(2x-1)≥0,解得 <x≤1,所以函数的定义域为(
<x≤1,所以函数的定义域为( ,1].
,1].
点评:考查学生理解函数定义域,并会根据二次根式的定义或对数函数的性质列不等式求解集的能力.
(2)也根据二次根式的定义及分母不为零,得到x的不等式求出解集即可;
(3)根据二次根式的定义及对数函数的性质,得到x的不等式求出解集即可.
解答:解:(1)由题得:x2-2x-3≥0 解得x≥3或x≤-1,所以函数的定义域为(-∞,-1]∪[3,+∞);
(2)由题知:2x-1>解得x>0,所以函数的定义域为(0,+∞).
(3)由题知:log
 (2x-1)≥0,解得
(2x-1)≥0,解得 <x≤1,所以函数的定义域为(
<x≤1,所以函数的定义域为( ,1].
,1].点评:考查学生理解函数定义域,并会根据二次根式的定义或对数函数的性质列不等式求解集的能力.

练习册系列答案
相关题目
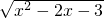

 .
.