题目内容

14．现有10张奖券，其中8张2元，2张5元，今某人随机无放回的抽取三张，则此人得奖金金额的数学期望为（　　）
A．6元B．12元C．7.8元D．9元

分析 求出奖金的可能值，求出概率，然后求解期望即可．

解答 解：现有10张奖券，其中8张2元，2张5元，今某人随机无放回的抽取三张，则此人得奖金金额的可能值为：6元，9元，12元，
它们的概率分别为：$\frac{{C}_{8}^{3}}{{C}_{10}^{3}}$=$\frac{7}{15}$，$\frac{{C}_{8}^{2}{C}_{2}^{1}}{{C}_{10}^{3}}$=$\frac{7}{15}$，$\frac{{C}_{8}^{1}{C}_{2}^{2}}{{C}_{10}^{3}}$=$\frac{1}{15}$．
此人得奖金金额的数学期望：6×$\frac{7}{15}$$+9×\frac{7}{15}$$+12×\frac{1}{15}$=7.8元．
故选：C．

点评 本题考查离散型随机变量的分布列的期望的求法，考查计算能力．

练习册系列答案
相关题目
4．已知函数f（x）=$\frac{\sqrt{2}}{2}$λsin（2x-$\frac{π}{4}$）+$\frac{λ}{2}$，x∈[-$\frac{3π}{8}$，$\frac{π}{4}$]，（λ≠0）．
（1）求函数f（x）的单调递增区间；
（2）当λ=2时，写出由函数y=sin2x的图象变换到与y=f（x）的图象的变换过程．
5．执行如图所示的程序框图，则输出的S值是（　　）
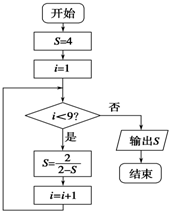
A．-1B．$\frac{2}{3}$C．$\frac{3}{2}$D．4
2．给出两个命题：命题p：不等式0＜α＜π成立是不等式sinα＞0成立的必要不充分条件；命题q：函数y=log2（$\sqrt{{x}^{2}+1}$-x）是奇函数，则下列命题是真命题的是（　　）
A．p∧qB．p∨￢qC．p∨qD．p∧￢q
9．函数y=ax2+bx与y=ax+b（a≠0，b≠0）画在一坐标系中的图象只可能是②③．（填序号）
19．在极坐标系中，圆ρ=8sinθ上的点到直线θ=$\frac{π}{3}$（ρ∈R）距离的最大值是6．
6．已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为（　　）
A．$\frac{2\sqrt{2}π}{3}$B．$\frac{4\sqrt{2}π}{3}$C．2$\sqrt{2}$πD．4$\sqrt{2}$π
3．如图，函数f（x）的图象为折线ACB，则不等式f（x）≥log2（x+1）的解集是（　　）
A．{x|-1＜x≤0}B．{x|-1≤x≤1}C．{x|-1＜x≤1}D．{x|-1＜x≤2}
4．若x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x-2y≤0}\\{x+2y-2≤0}\end{array}\right.$，则z=x+y的最大值为$\frac{3}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网