题目内容
已知数列{an}满足a1=1,an+1=2an+1(n∈N*).(1)求数列{an}的通项公式;
(2)若数列{bn}满足
…
=
(n∈N*),证明{bn}是等差数列；
(3)证明
（n∈N*）.
（1）解:∵an+1=2an+1（n∈N*），
∴an+1+1=2（an+1）.∴{an+1}是以a1+1=2为首项，2为公比的等比数列.
∴an+1+=2n，即an=2n-1（n∈N*）.
（2）证明:证法1：∵…=，
∴=
，
∴2［（b1+b2+…+bn）-n］=nbn，①
2［（b1+b2+…+bn+bn+1）-（n+1）］=（n+1）bn+1，②
②-①，得2（bn+1-1）=（n+1）bn+1-nbn，
即（n-1）bn+1-nbn+2=0，③
nbn+2-（n+1）bn+1+2=0.④
④-③，得nbn+2-2nbn-1+nbn=0.
即bn+2-2bn+1+bn=0，
∴bn+2-bn+1=bn+1-bn（n∈N*）.
∴{bn}是等差数列.
证法2：同证法1，
得（n-1）bn+1-nbn+2=0.
令n=1，得b1=2.
设b2=2+d（d∈R），下面用数学归纳法证明bn=2+（n-1）d.
①当n=1、2时，等式成立.
②假设当n=k（k≥2）时，
bk=2+k-1）d，
那么bk+1=
［2+（k-1）d］-
=2+［（k+1）-1］d.
这就是说，当n=k+1时，等式也成立.
根据①和②，可知bn=2+（n-1）d对任何n∈N*都成立.
∵bn+1-bn=d，∴{bn}是等差数列.
（3）证明：∵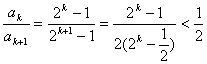
，k=1，2，…，n，
∴
.
∵
,k=1，2，…，n，
∴
.
∴
（n∈N*）.
练习册系列答案
相关题目