题目内容
如图,在由圆O:x2+y2=1和椭圆C: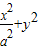 =1(a>1)构成的“眼形”结构中,已知椭圆的离心率为
=1(a>1)构成的“眼形”结构中,已知椭圆的离心率为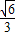 ,直线l与圆O相切于点M,与椭圆C相交于两点A,B.
,直线l与圆O相切于点M,与椭圆C相交于两点A,B.(1)求椭圆C的方程;
(2)是否存在直线l,使得
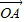 •
•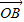 =
=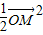 ,若存在,求此时直线l的方程;若不存在,请说明理由.
,若存在,求此时直线l的方程;若不存在,请说明理由.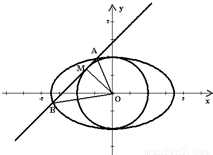
【答案】分析:(1)根据椭圆C: =1(a>1)的离心率为
=1(a>1)的离心率为 ,可得a2=3,从而可求椭圆C的方程;
,可得a2=3,从而可求椭圆C的方程;
(2)假设存在直线l,使得 •
• =
= ,当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,由直线l与圆O相切,可得b2=k2+1,代入椭圆C的方程为
,当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,由直线l与圆O相切,可得b2=k2+1,代入椭圆C的方程为 ,可得(1+3k2)x2+6kbx+3b2-3=0
,可得(1+3k2)x2+6kbx+3b2-3=0
设A(x1,y1)、B(x2,y2),进而利用 •
• =
= ,即可知存在直线l.
,即可知存在直线l.
解答:解:(1)∵椭圆C: =1(a>1)的离心率为
=1(a>1)的离心率为 ,
,
∴
解得:a2=3,所以所求椭圆C的方程为 (5分)
(5分)
(2)假设存在直线l,使得 •
• =
= ,
,
当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,
由直线l与圆O相切,可得b2=k2+1 …(1)(7分)
代入椭圆C的方程为 ,可得(1+3k2)x2+6kbx+3b2-3=0
,可得(1+3k2)x2+6kbx+3b2-3=0
设设A(x1,y1)、B(x2,y2),则 ,
,
∴ =
= =
= …(2)
…(2)
由(1)(2)可得k2=1,b2=2
故存在直线l,方程为 ,使得
,使得 •
• =
= .
.
点评:本题以椭圆的几何性质为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,同时考查了存在性问题,合理运用向量的数量积运算是解题的关键.
 =1(a>1)的离心率为
=1(a>1)的离心率为 ,可得a2=3,从而可求椭圆C的方程;
,可得a2=3,从而可求椭圆C的方程;(2)假设存在直线l,使得
 •
• =
= ,当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,由直线l与圆O相切,可得b2=k2+1,代入椭圆C的方程为
,当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,由直线l与圆O相切,可得b2=k2+1,代入椭圆C的方程为 ,可得(1+3k2)x2+6kbx+3b2-3=0
,可得(1+3k2)x2+6kbx+3b2-3=0设A(x1,y1)、B(x2,y2),进而利用
 •
• =
= ,即可知存在直线l.
,即可知存在直线l.解答:解:(1)∵椭圆C:
 =1(a>1)的离心率为
=1(a>1)的离心率为 ,
,∴

解得:a2=3,所以所求椭圆C的方程为
 (5分)
(5分)(2)假设存在直线l,使得
 •
• =
= ,
,当直线l垂直于x轴时,不符合题意,故设直线l方程为y=kx+b,
由直线l与圆O相切,可得b2=k2+1 …(1)(7分)
代入椭圆C的方程为
 ,可得(1+3k2)x2+6kbx+3b2-3=0
,可得(1+3k2)x2+6kbx+3b2-3=0设设A(x1,y1)、B(x2,y2),则
 ,
,
∴
 =
= =
= …(2)
…(2)由(1)(2)可得k2=1,b2=2
故存在直线l,方程为
 ,使得
,使得 •
• =
= .
.点评:本题以椭圆的几何性质为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,同时考查了存在性问题,合理运用向量的数量积运算是解题的关键.

练习册系列答案
相关题目
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: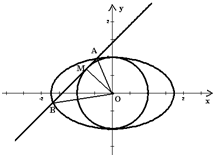 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: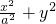 =1(a>1)构成的“眼形”结构中,已知椭圆的离心率为
=1(a>1)构成的“眼形”结构中,已知椭圆的离心率为 ,直线l与圆O相切于点M,与椭圆C相交于两点A,B.
,直线l与圆O相切于点M,与椭圆C相交于两点A,B. •
• =
=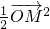 ,若存在,求此时直线l的方程;若不存在,请说明理由.
,若存在,求此时直线l的方程;若不存在,请说明理由.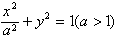 构成的“眼形”结构中,已知椭圆的离心率为
构成的“眼形”结构中,已知椭圆的离心率为 ,直线l与圆O相切于点M,与椭圆C相交于A、B两点.
,直线l与圆O相切于点M,与椭圆C相交于A、B两点. 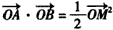 ,若存在,求此时直线l的方程;若不存在,请说明理由.
,若存在,求此时直线l的方程;若不存在,请说明理由. 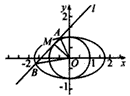
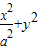 =1(a>1)构成的“眼形”结构中,已知椭圆的离心率为
=1(a>1)构成的“眼形”结构中,已知椭圆的离心率为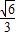 ,直线l与圆O相切于点M,与椭圆C相交于两点A,B.
,直线l与圆O相切于点M,与椭圆C相交于两点A,B.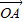 •
•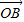 =
=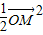 ,若存在,求此时直线l的方程;若不存在,请说明理由.
,若存在,求此时直线l的方程;若不存在,请说明理由.