题目内容
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.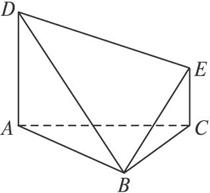
(1)求证:平面ADB⊥平面EDB;
(2)求直线BC与平面EDB所成角的正弦值.
(1)证明:分别取BD、AB中点F、G,连EF,FG,GC![]() CE∥FG,CE=FG
CE∥FG,CE=FG![]() EF∥CG,
EF∥CG,
CG⊥AB,CG⊥平面ADB![]() EF⊥平面ADB,EF
EF⊥平面ADB,EF![]() 平面BDE
平面BDE![]() 平面EDB⊥平面ADB.
平面EDB⊥平面ADB.
(2)解:VC—BDE=VD—BCE,S△BDE=![]() ,S△BCE=1.
,S△BCE=1.
D到平面BCE的距离=A到平面BCE的距离=![]() .
.
![]() ·h·
·h·![]() =
=![]() ·
·![]() ·1
·1![]() h=
h=![]() .
.
设θ为直线BC与平面EDB所成角![]() sinθ=
sinθ=![]() =
=![]() .
.

练习册系列答案
相关题目
 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=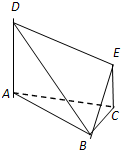 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1. 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.
在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.