题目内容
(本小题满分12分)
已知函数f(x)=x2(x-3a)+1 (a>0,x∈R).
(a>0,x∈R).
(I)求函数y=f(x)的极值;
(II)函数y=f(x)在(0,2)上单调 递减,求实数a的取值范围;
递减,求实数a的取值范围;
(III)若在区间(0,+∞)上存在实数x0,使得不等式f(x0)-4a3≤0能成立,求实数a的取值范围.
【答案】
(I)当a>0时,在x=0处,函数f(x)有极大值f(0)=1;在x=2a处,函数f(x)有极小值f(2a)=-4a3+1 .
(II)a≥1
(III)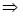 a≥
a≥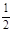 .
.
【解析】解:f'(x)=3x(x-2a),令f'(x)=0,得x=0或x=2a .
f(0)=1,f(2a)=-4a3+1 .
(I)当a>0时,2a>0,当x变化时,f'(x),f(x)的变化情况如下 表:
表:
|
x |
(-∞,0) |
0 |
(0,2a) |
2a |
(2a,+∞) |
|
f'(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
1 |
↘ |
-4a3+1 |
↗ |
∴ 当a>0时,在x=0处,函数f(x)有极大值f(0)=1;在x=2a处,函数f(x)有极小值f(2a)=-4a3+1 .
(II)在(0,2)上单调递减,∴ 2a≥2,即a≥1 .
(III)依题意得 4a3≥f(x)min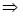 4a3≥-4a3+1
4a3≥-4a3+1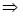 8a3≥1
8a3≥1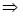 a≥
a≥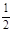 .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目