题目内容
已知等比数列{an}的公比为q,前n项和为Sn,若S2011,S2010,S2012成等差数列,且S1=1,则an=________.
(-2)n-1
分析:首先讨论当等比数列q=1是否满足题干条件,然后讨论当q≠1时,由S2011,S2010,S2012成等差数列,求出q的值,再求出等比数列的通项公式.
解答:当等比数列的公比q=1时,
若S2011,S2010,S2012成等差数列,
则2×2010a1=2011a1+2012a1,
解得a1≠S1=1,
故q≠1,
当q≠1时,若S2011,S2010,S2012成等差数列,a1=S1=1,
则2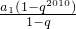 =
=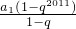 +
+ ,
,
解得q=-2,
∴an=(-2)n-1,
故答案为:an=(-2)n-1.
点评:本题主要考查数列递推式的知识点,解答本题的关键是求出等比数列的公比q,此题难度不是很大.
分析:首先讨论当等比数列q=1是否满足题干条件,然后讨论当q≠1时,由S2011,S2010,S2012成等差数列,求出q的值,再求出等比数列的通项公式.
解答:当等比数列的公比q=1时,
若S2011,S2010,S2012成等差数列,
则2×2010a1=2011a1+2012a1,
解得a1≠S1=1,
故q≠1,
当q≠1时,若S2011,S2010,S2012成等差数列,a1=S1=1,
则2
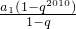 =
=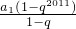 +
+ ,
,解得q=-2,
∴an=(-2)n-1,
故答案为:an=(-2)n-1.
点评:本题主要考查数列递推式的知识点,解答本题的关键是求出等比数列的公比q,此题难度不是很大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目