题目内容
设抛物线y2=2px(p为常数)的准线与X轴交于点K,过K的直线l与抛物线交于A、B两点,则
•
=
p2
p2.
| OA |
| OB |
| 5 |
| 4 |
| 5 |
| 4 |
分析:设点A(x1,y1),B(x2,y2).设直线l:my=x+
.联立
化为y2-2pmy+p2=0.由于直线l与抛物线相交于不同两点,得到△>0,化为m2>1.利用根与系数的关系y1+y2=2pm,y1y2=p2.再利用数量积运算可得
•
=x1x2+y1y2=(my1-
)(my2-
)+y1y2,代入即可.
| p |
| 2 |
|
| OA |
| OB |
| p |
| 2 |
| p |
| 2 |
解答:解:如图所示,
设点A(x1,y1),B(x2,y2).
设直线l:my=x+
.
联立
化为y2-2pmy+p2=0.
∵直线l与抛物线相交于不同两点,∴△>0,化为m2>1.
∴y1+y2=2pm,y1y2=p2.
∴
•
=x1x2+y1y2=(my1-
)(my2-
)+y1y2
=(m2+1)y1y2-
(y1+y2)+
=(m2+1)•p2-
•2pm+
=
p2.
故答案为
p2.

设点A(x1,y1),B(x2,y2).
设直线l:my=x+
| p |
| 2 |
联立
|
∵直线l与抛物线相交于不同两点,∴△>0,化为m2>1.
∴y1+y2=2pm,y1y2=p2.
∴
| OA |
| OB |
| p |
| 2 |
| p |
| 2 |
=(m2+1)y1y2-
| pm |
| 2 |
| p2 |
| 4 |
=(m2+1)•p2-
| pm |
| 2 |
| p2 |
| 4 |
=
| 5 |
| 4 |
故答案为
| 5 |
| 4 |
点评:熟练掌握直线与抛物线相交问题转化方程联立得到关于一个未知数的一元二次方程得根与系数的关系、数量积得运算法则等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
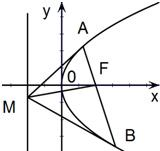 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)