题目内容
如图,边长为3(百米)的正方形ABCD是一个观光区的平面示意图,中间叶形阴影部分MN是一片人工湖,它的左下方边缘曲线段MN为函数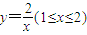 的图象.为了便于游客观光,拟在观光区内铺设一条穿越该区域的直路l(宽度不计),其与人工湖左下方曲线段MN相切(切点记为P),并把该区域分为两部分.现直路l左下部分区域规划为花圃,记点P到边AD距离为t,f(t)表示花圃的面积.
的图象.为了便于游客观光,拟在观光区内铺设一条穿越该区域的直路l(宽度不计),其与人工湖左下方曲线段MN相切(切点记为P),并把该区域分为两部分.现直路l左下部分区域规划为花圃,记点P到边AD距离为t,f(t)表示花圃的面积.(1)求直路l所在的直线与两坐标轴的交点坐标;
(2)求面积f(t)的解析式;
(3)请你制定一个铺设方案,使得花圃面积最大,并求出最大值.
【答案】分析:(1)求导函数,确定过点P的切线方程,即可求得直线与两坐标轴的交点坐标;
(2)分类讨论:①当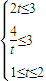 ,即
,即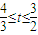 时,切线左下方的区域为一直角三角形;②当
时,切线左下方的区域为一直角三角形;②当 ,即
,即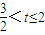 时,切线左下方的区域为一直角梯形;③当
时,切线左下方的区域为一直角梯形;③当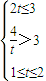 ,即
,即 时,切线左下方的区域为一直角梯形,从而可得面积f(t)的解析式;
时,切线左下方的区域为一直角梯形,从而可得面积f(t)的解析式;
(3)求出分段函数的最值,即可得到花圃面积最大值.
解答:解:(1)求导函数可得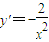
∴过点P的切线方程为 ,即
,即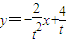
令x=0可得y= ,令y=0可得x=2t
,令y=0可得x=2t
∴切线与x轴交点坐标为(2t,0),与y轴交点坐标为(0, )
)
(2)①当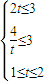 ,即
,即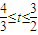 时,切线左下方的区域为一直角三角形
时,切线左下方的区域为一直角三角形
∴f(t)= =4;
=4;
②当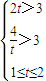 ,即
,即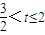 时,切线左下方的区域为一直角梯形
时,切线左下方的区域为一直角梯形
∴f(t)=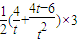 =
=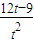 ;
;
③当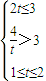 ,即
,即 时,切线左下方的区域为一直角梯形
时,切线左下方的区域为一直角梯形
∴f(t)= =
=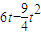 ;
;
综上,f(t)=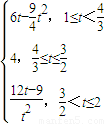 ;
;
(3)当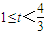 时,f(t)=
时,f(t)= =-
=- ;
;
当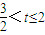 时,f(t)=
时,f(t)=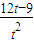 =
=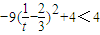 ;
;
当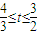 时,f(t)=4是常数;
时,f(t)=4是常数;
综上,当 时,花圃面积最大,最大值为4.
时,花圃面积最大,最大值为4.
点评:本题考查导数的几何意义,考查函数解析式的确定,考查分段函数的最值,正确分类是关键.
(2)分类讨论:①当
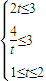 ,即
,即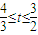 时,切线左下方的区域为一直角三角形;②当
时,切线左下方的区域为一直角三角形;②当 ,即
,即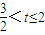 时,切线左下方的区域为一直角梯形;③当
时,切线左下方的区域为一直角梯形;③当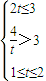 ,即
,即 时,切线左下方的区域为一直角梯形,从而可得面积f(t)的解析式;
时,切线左下方的区域为一直角梯形,从而可得面积f(t)的解析式;(3)求出分段函数的最值,即可得到花圃面积最大值.
解答:解:(1)求导函数可得
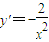
∴过点P的切线方程为
 ,即
,即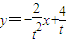
令x=0可得y=
 ,令y=0可得x=2t
,令y=0可得x=2t∴切线与x轴交点坐标为(2t,0),与y轴交点坐标为(0,
 )
)(2)①当
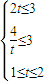 ,即
,即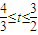 时,切线左下方的区域为一直角三角形
时,切线左下方的区域为一直角三角形∴f(t)=
 =4;
=4;②当
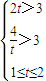 ,即
,即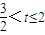 时,切线左下方的区域为一直角梯形
时,切线左下方的区域为一直角梯形∴f(t)=
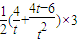 =
=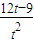 ;
;③当
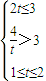 ,即
,即 时,切线左下方的区域为一直角梯形
时,切线左下方的区域为一直角梯形∴f(t)=
 =
=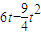 ;
;综上,f(t)=
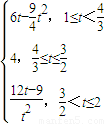 ;
;(3)当
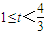 时,f(t)=
时,f(t)= =-
=- ;
;当
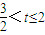 时,f(t)=
时,f(t)=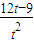 =
=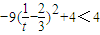 ;
;当
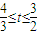 时,f(t)=4是常数;
时,f(t)=4是常数;综上,当
 时,花圃面积最大,最大值为4.
时,花圃面积最大,最大值为4.点评:本题考查导数的几何意义,考查函数解析式的确定,考查分段函数的最值,正确分类是关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目