题目内容
2.A,B,O是平面内不共线的三个定点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点P关于点A的对称点为Q,点Q关于点B的对称点为R,则$\overrightarrow{PR}$等于( )| A. | $\overrightarrow{a}$-$\overrightarrow{b}$ | B. | 2($\overrightarrow{b}$-$\overrightarrow{a}$) | C. | 2($\overrightarrow{a}$-$\overrightarrow{b}$) | D. | $\overrightarrow{b}$-$\overrightarrow{a}$ |
分析 根据向量的平行四边形法则即可求出.
解答 解:根据向量的平行四边形法则得
2$\overrightarrow{a}$=$\overrightarrow{OP}$+$\overrightarrow{OQ}$,2$\overrightarrow{b}$=$\overrightarrow{OQ}$+$\overrightarrow{OR}$,
∴2($\overrightarrow{b}$-$\overrightarrow{a}$)=$\overrightarrow{OR}$-$\overrightarrow{OP}$=$\overrightarrow{PR}$
故选:B.
点评 本题考查了平行四边形法则,以及向量加减的几何意义,属于基题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
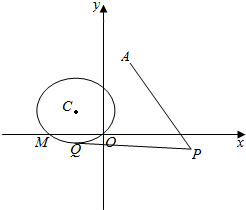 圆C过点M(-2,0)及原点,且圆心C在直线x+y=0上.
圆C过点M(-2,0)及原点,且圆心C在直线x+y=0上.