题目内容
已知A、B为抛物线C:y2=4x上的不同两点,F为抛物线C的焦点,若 ,则直线AB的斜率为
,则直线AB的斜率为
- A.

- B.

- C.
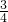
- D.
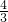
D
分析:先设点A,B的坐标,求出直线方程后与抛物线方程联立消去y得到关于x的一元二次方程,求出两根,再根据向量的有关知识得到坐标的关系,进而代入抛物线的方程中得到答案.
解答:由题意可知直线的斜存在,故可设为k(k≠0)
∵抛物线 C:y2=4x焦点F(1,0),准线x=-1,则直线AB的方程为y=k(x-1)
联立方程 可得k2x2-2(2+k2)x+k2=0
可得k2x2-2(2+k2)x+k2=0
设A(x1,y1),B(x2,y2),则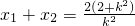 ,y1+y2=k(x1+x2-2)=
,y1+y2=k(x1+x2-2)=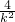 •k=
•k=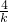
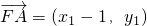 ,
,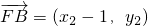
∵ ,
,
∴ 即
即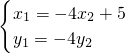 ②
②
①②联立可得,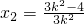 ,
,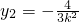
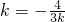 ,代入抛物线方程y2=4x可得
,代入抛物线方程y2=4x可得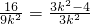 ×4
×4
∴9k2=16
∴
故选D
点评:本题主要考查直线与抛物线的位置关系,抛物线定义的应用以及向量的有关知识.
分析:先设点A,B的坐标,求出直线方程后与抛物线方程联立消去y得到关于x的一元二次方程,求出两根,再根据向量的有关知识得到坐标的关系,进而代入抛物线的方程中得到答案.
解答:由题意可知直线的斜存在,故可设为k(k≠0)
∵抛物线 C:y2=4x焦点F(1,0),准线x=-1,则直线AB的方程为y=k(x-1)
联立方程
 可得k2x2-2(2+k2)x+k2=0
可得k2x2-2(2+k2)x+k2=0设A(x1,y1),B(x2,y2),则
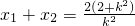 ,y1+y2=k(x1+x2-2)=
,y1+y2=k(x1+x2-2)=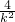 •k=
•k=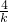
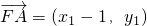 ,
,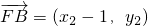
∵
 ,
,∴
 即
即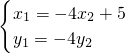 ②
②①②联立可得,
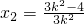 ,
,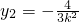
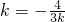 ,代入抛物线方程y2=4x可得
,代入抛物线方程y2=4x可得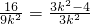 ×4
×4∴9k2=16
∴

故选D
点评:本题主要考查直线与抛物线的位置关系,抛物线定义的应用以及向量的有关知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则直线AB的斜率为( )
,则直线AB的斜率为( )



 ,则直线AB的斜率为( )
,则直线AB的斜率为( )



 ,则直线AB的斜率为( )
,则直线AB的斜率为( )

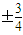

 ,则直线AB的斜率为( )
,则直线AB的斜率为( )


