题目内容
如图,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体。经过搅拌后,从中随机取出一个小正方体,记它的涂油漆面数为 ,则
,则 的均值为
的均值为
A. | B. | C. | D. |

B
解析试题分析:由题意可知:X所有可能取值为0,1,2,3.①8个顶点处的8个小正方体涂有3面,∴P(X=3)= ;
;
②每一条棱上除了两个顶点处的小正方体,还剩下3个,一共有3×12=36个小正方体涂有2面,∴P(X=2)= ;
;
③每个表面去掉四条棱上的16个小正方形,还剩下9个小正方形,因此一共有9×6=54个小正方体涂有一面,∴P(X=1)=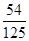 .
.
④由以上可知:还剩下125-(8+36+54)=27个内部的小正方体的6个面都没有涂油漆,
∴P(X=0)= .
.
故X的分布列为X 0 1 2 3 P 
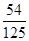


因此E(X)=0× +1×
+1×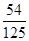 +2×
+2× +3×
+3× =
= .故选B.
.故选B.
考点:离散型随机变量的期望与方差.

练习册系列答案
相关题目
已知随机变量 服从正态分布N(2,σ2),且P(
服从正态分布N(2,σ2),且P( <4)=0.8,则P(0<
<4)=0.8,则P(0< <2)=( )
<2)=( )
| A.0.6 | B.0.4 | C.0.3 | D.0.2 |
随机变量 的概率分布列规律为
的概率分布列规律为 其中
其中 为常数,则
为常数,则 的值为 ( ).
的值为 ( ).
A. | B. | C. | D. |
签盒中有编号为1,2,3,4,5,6的六支签,从中任意取3支,设X为这3支签的号码之中最大的一个,则X的数学期望为( )
| A.5 | B.5.25 | C.5.8 | D.4.6 |
 的展开式中,前三项的系数成等差数列
的展开式中,前三项的系数成等差数列
 B.
B.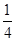 C.
C. D.
D.





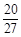
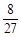

 展开式的二项式系数和为512,
展开式的二项式系数和为512,
 的值;
的值; 的值;
的值; 被6整除的余数.
被6整除的余数.