题目内容
将7×7的棋盘中的2个方格染成黄色,其余的染成绿色.若一种染色法经过在棋盘的平面中旋转而得到,那么这两种染色法看着是同一种,则有 种不同的染色法.
【答案】分析:根据是7×7棋盘,有4条对称轴,不同染色法有  种,还有对称轴上关于中心对称的情况
种,还有对称轴上关于中心对称的情况 种,把这两个数相加,即得所求.
种,把这两个数相加,即得所求.
解答:解:因为是7×7棋盘,有4条对称轴,不同染色法有 =294种,
=294种,
还有对称轴上关于中心对称的情况 12÷2=6 种,
故一共有294+6=300种,
故答案为 300.
点评:本题主要考查排列、组合以及两个基本原理的应用,要特别注意重复的情况,属于中档题.
 种,还有对称轴上关于中心对称的情况
种,还有对称轴上关于中心对称的情况 种,把这两个数相加,即得所求.
种,把这两个数相加,即得所求.解答:解:因为是7×7棋盘,有4条对称轴,不同染色法有
 =294种,
=294种,还有对称轴上关于中心对称的情况 12÷2=6 种,
故一共有294+6=300种,
故答案为 300.
点评:本题主要考查排列、组合以及两个基本原理的应用,要特别注意重复的情况,属于中档题.

练习册系列答案
相关题目
为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个50m2的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
表2:不施用新化肥小麦产量频数分布表
(1)完成下面频率分布直方图;


施用新化肥后小麦产量的频率分布直方图 不施用新化肥后小麦产量的频率分布直方图
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量;
(3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3:
附:
表1:施用新化肥小麦产量频数分布表
| 小麦产量 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) |
| 频数 | 10 | 35 | 40 | 10 | 5 |
| 小麦产量 | [0,10) | [10,20) | [20,30) | [30,40) |
| 频数 | 15 | 50 | 30 | 5 |


施用新化肥后小麦产量的频率分布直方图 不施用新化肥后小麦产量的频率分布直方图
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量;
(3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3:
| 小麦产量小于20kg | 小麦产量不小于20kg | 合计 | |
| 施用新化肥 | a= | b= | |
| 不施用新化肥 | c= | d= | |
| 合计 | n= |

| P(K2≥k) | 0.050 0.010 0.005 0.001 |
| k | 3.841 6.635 7.879 10.828 |
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据建立一个2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1,2,3,4,5,某5名爱看课外书且作文水平一般的学生也分别编号为1,2,3,4,5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附:
临界值表:
(Ⅰ)试根据以上数据建立一个2×2列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1,2,3,4,5,某5名爱看课外书且作文水平一般的学生也分别编号为1,2,3,4,5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
附:

临界值表:
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 (7)转换成十进制形式是( )
(7)转换成十进制形式是( )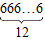 (7)转换成十进制形式是( )
(7)转换成十进制形式是( )