Question

两平行平面去截球，如图,在两个截面圆上有两个点，它们的球坐标分别为A(25,arctan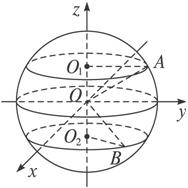,θ_a),B(25,π-arctan,θ_b)，

求出这两个截面间的距离.

Answer 1

解:由已知,OA=OB=25,∠AOO₁=arctan,∠BOO₁=π-arctan,在△AOO₁中,tan∠AOO₁==.

∵OA=25,∴OO₁=7.

在△BOO₂中,∠BOO₂=arctan,tan∠BOO₂==.

∵OB=25,∴OO₂=20.

则O₁O₂=OO₁+OO₂=7+20=27.

∴两个截面间的距离O₁O₂为27.