Question

定义“等积数列”为：数列{a_n}中，对任意n∈N^*，都有a_na_n+1=p（常数），则数列{a_n}称为等积数列，p为公积，现已知数列{a_n}为等积数列，且a₁=1，a₂=2，则当n为奇数时，前n项和s_n=________．

Answer 1

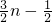
分析：先利用定义求出数列{a_n}的各项的规律：即所有奇数项为1，所有偶数项为2．再分析出当n为奇数时，奇数项的个数和偶数项的个数，再代入求和公式即可．
解答：由定义得，数列{a_n}的各项为1，2，1，2，1，2…
即所有奇数项为1，所有偶数项为2．
又因为当n为奇数时，其前n项中有个1，有个2，
所以 s_n=+2×=-．
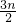故答案为 -．
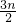点评：本题的关键点在于找到数列{a_n}中所有奇数项为1，所有偶数项为2．易错点在于分析不了当n为奇数时，找不出奇数项的个数和偶数项的个数．