题目内容
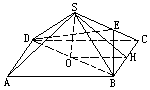
如图,在正四棱锥S-ABCD中,高SO=a,底面边长为2a,求:
(1)侧面与底面夹角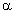 ;
;
(2)顶点A到侧棱SC的距离;
(3)相邻两侧面的夹角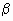 .
.
答案:
解析:
解析:
|
解 (1)由SO⊥底面ABCD,知O为底面正方形ABCD的中心.过O作OH⊥BC于H,连结SH(图).由三垂线定理,可知BC⊥SH,故∠SHO为侧面与底面所成二面角的平面角,即∠SHO=
(2)SA=SC=
(3)过B作BE⊥SC于E,连结DE.由△BEC≌△DEC,得∠DEC=∠BEC= 在△BED中, |

练习册系列答案
相关题目
 .在Rt△SOH中,SO=OH=a,故∠SHO=
.在Rt△SOH中,SO=OH=a,故∠SHO= ,即
,即
 a,AC=
a,AC= a,cos∠ASC=-
a,cos∠ASC=- .过A作AF⊥CS的延长线于F(图),则cos∠ASF=
.过A作AF⊥CS的延长线于F(图),则cos∠ASF= ,故可得d=AS·sin∠ASF=
,故可得d=AS·sin∠ASF= a,即A到SC的距离为
a,即A到SC的距离为 a.
a.
 ,故DE⊥SC,∠BED为二面角B-SC-D的平面角,
,故DE⊥SC,∠BED为二面角B-SC-D的平面角,

 .又0<
.又0< <
< ,故
,故 .
.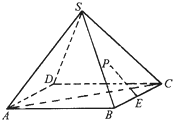 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( ) 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为( )
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为( ) 如图,在正四棱锥S-ABCD中,AB=
如图,在正四棱锥S-ABCD中,AB= 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )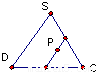
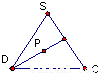
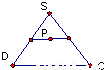
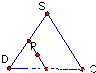
 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )