题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 有唯一零点,求
有唯一零点,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)![]() 时,求出导函数,求出
时,求出导函数,求出![]() ,将
,将![]() 代入到
代入到![]() 中得到曲线
中得到曲线![]() 在点
在点![]() 处的切线的斜率,求出
处的切线的斜率,求出![]() ,然后利用点斜式求出曲线
,然后利用点斜式求出曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(Ⅱ)先利用导数证明函数![]() 在R上有唯一零点
在R上有唯一零点![]() ,且函数
,且函数![]() 在
在![]() 上递,在
上递,在![]() 上递增,所以函数
上递增,所以函数![]() 在
在![]() 处取得最小值
处取得最小值![]() ,再根据函数
,再根据函数![]() 有唯一零点可得
有唯一零点可得![]() ,然后根据
,然后根据![]() 以及
以及![]() 联立消去
联立消去![]() ,得到
,得到![]() ,然后构造函数
,然后构造函数![]() ,通过导数的方法可得
,通过导数的方法可得![]() 有唯一零点
有唯一零点![]() ,且
,且![]() ,最后将
,最后将![]() 代入到
代入到![]() 可以解得
可以解得![]() 的值.
的值.
(Ⅰ)当![]() 时,
时,![]() .
.
![]() .
.
![]() .
.
又![]() ,
,
![]() 曲线
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(Ⅱ)![]()
![]() .
.
令![]() ,则
,则![]() .
.
![]() ,
,![]() 函数
函数![]() 在
在![]() 仅有一个零点.
仅有一个零点.
![]() 存在
存在![]() ,使得
,使得![]() .
.
即存在![]() 满足
满足![]() 时,
时,![]() .
.
![]() 当
当![]() ,即
,即![]() 时,
时,![]() .
.
![]() 在
在![]() 上单调递减;
上单调递减;
当![]() ,即
,即![]() 时,
时,![]() .
.
![]() 在
在![]() 上单调递增.
上单调递增.
又当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]()
![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,![]() 当
当![]() 时,
时,![]() .
.
![]() 由题意,函数
由题意,函数![]() 有唯一零点时,必有
有唯一零点时,必有![]() .①
.①
又![]() ,②
,②
由①②消去![]() ,得
,得![]() .
.
令![]() .
.![]() ,
,![]() 单调递增.
单调递增.
又![]() ,
,
![]() 方程
方程![]() 有唯一解
有唯一解![]() .
.
将![]() 代入
代入![]() ,解得
,解得![]() .
.
![]() 当函数
当函数![]() 有唯一零点时,
有唯一零点时,![]() 的值为
的值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某企业为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取![]() 件产品作为样本称出它们的质量(单位:毫克),质量值落在
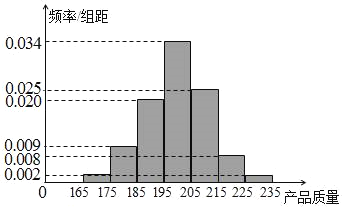
件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)以样本的频率作为概率,试估计从甲流水线上任取![]() 件产品,求其中不合格品的件数
件产品,求其中不合格品的件数![]() 的数学期望.
的数学期望.
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
(Ⅱ)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
(Ⅲ)由乙流水线的频率分布直方图可以认为乙流水线生产的产品质量![]() 服从正态分布
服从正态分布![]() ,求质量
,求质量![]() 落在
落在![]() 上的概率.
上的概率.
参考公式:![]()
![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
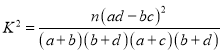 ,其中
,其中![]() .
.

