题目内容
如果一个点是一个指数函数和一个对数函数的图象的交点,那么称这个点为“好点”.下列五个点P1(1,1),P2(1,2), ,P4(2,2),
,P4(2,2), 中,“好点”是________(写出所有的好点).
中,“好点”是________(写出所有的好点).
P3,P4,P5
分析:利用指数函数的性质,易得P1(1,1),P2(1,2)不是好点,利用“好点”的定义,我们易构造指数方程和对数方程,得到 ,P4(2,2),
,P4(2,2), 三个点是好点,从而得到答案.
三个点是好点,从而得到答案.
解答:当x=1时,对数函数y=logax(a>0,a≠1)恒过(1,0)点,
故P1(1,1),P2(1,2)一定不是好点,
而 是函数y=
是函数y= 与y=
与y=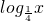 的交点;
的交点;
P4(2,2)是函数y= 与y=
与y= 的交点;
的交点;
 是函数y=4x与y=
是函数y=4x与y= 的交点;
的交点;
故答案为P3,P4,P5
点评:本题考查的知识点是指数函数与对数函数的性质,利用指数函数和对数的性质,排除掉不满足“好点”定义的点是解答本题的关键.
分析:利用指数函数的性质,易得P1(1,1),P2(1,2)不是好点,利用“好点”的定义,我们易构造指数方程和对数方程,得到
 ,P4(2,2),
,P4(2,2), 三个点是好点,从而得到答案.
三个点是好点,从而得到答案.解答:当x=1时,对数函数y=logax(a>0,a≠1)恒过(1,0)点,
故P1(1,1),P2(1,2)一定不是好点,
而
 是函数y=
是函数y= 与y=
与y=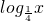 的交点;
的交点;P4(2,2)是函数y=
 与y=
与y= 的交点;
的交点; 是函数y=4x与y=
是函数y=4x与y= 的交点;
的交点;故答案为P3,P4,P5
点评:本题考查的知识点是指数函数与对数函数的性质,利用指数函数和对数的性质,排除掉不满足“好点”定义的点是解答本题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好点”.在下面的五个点M(1,1),N(1,2),P(2,1),Q(2,2),G(2,0.5)中,“好点”的个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |