题目内容
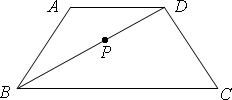
如图，已知等腰梯形ABCD的三边AB、BC、CD分别与函数
的图象切于点P、Q、R，且点P的横坐标为t（0<t≤2）.
（Ⅰ）试求直线AB的方程；
（Ⅱ）试求点P的坐标，使得梯形ABCD的面积最小，并求出梯形面积的最小值.
解：（Ⅰ）由题意得，点P的坐标为
点Q的坐标为（0，2）
∵
即直线AB的斜率为－t
∴直线AB的方程为
，
即 
（Ⅱ）设梯形ABCD的面积为S，由（Ⅰ）知直线AB的方程为
令y=0 得，
又直线BC的方程为y=2，可得：
∴
当且仅当
∴t=
时，S有最小值为4. 此时P点的坐标为（，1）
∴当P点的坐标为（，1）时，梯形ABCD的面积有最小值，最小值为4
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
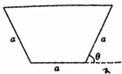汶川大地震后，为了消除某堰塞湖可能造成的危险，救授指挥部商定，给该堰塞湖挖一个横截面为等腰梯形的简易引水槽（如图所示）进行引流，已知等腰梯形的下底与腰的长度都为a，且水槽的单位时间内的最大流量与横载面的面积为正比，比例系数k＞0．
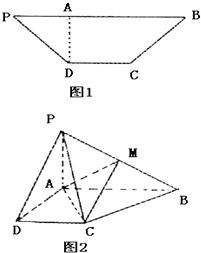已知等腰梯形PDCB中（如图1），PB=3，DC=1，PB=BC=
如图，已知ABCD是底角为30°的等腰梯形，AD=2
如图，已知A（-2，0），B（2，0），等腰梯形ABCD满足|AB|=-2|CD|，E为AC上一点，且
