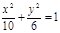题目内容
若椭圆的两焦点为(-2,0)和(2,0),且椭圆过点(
,-
),则椭圆方程是
+
=1
+
=1.
| 5 |
| 2 |
| 3 |
| 2 |
| x2 |
| 10 |
| y2 |
| 6 |
| x2 |
| 10 |
| y2 |
| 6 |
分析:设椭圆方程为:
+
=1(a>b>0),由焦点坐标可得c值,由椭圆定义即可求得a,根据b2=a2-c2可求得b值.
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:设椭圆方程为:
+
=1(a>b>0),
则c=2,且2a=
+
=2
,解得a=
,
所以b2=a2-c2=(
)2-22=6,
所以椭圆方程为
+
=1.
故答案为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
则c=2,且2a=
(
|
(
|
| 10 |
| 10 |
所以b2=a2-c2=(
| 10 |
所以椭圆方程为
| x2 |
| 10 |
| y2 |
| 6 |
故答案为
| x2 |
| 10 |
| y2 |
| 6 |
点评:本题考查椭圆定义及其标准方程的求解,属基础题,熟记椭圆定义及方程各字母意义是解决问题的基础.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若椭圆的两焦点为(-2,0)和(2,0),且椭圆过点(
,-
),则椭圆方程是( )
| 5 |
| 2 |
| 3 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
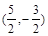 ,则椭圆方程是( )
,则椭圆方程是( ) B.
B.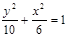 C.
C. D.
D.
 ,则椭圆方程是( )
,则椭圆方程是( ) B.
B. C.
C. D.
D.
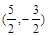 ,则椭圆方程是 (
)
,则椭圆方程是 (
)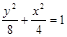 B.
B.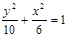 C.
C.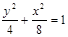 D.
D.