题目内容

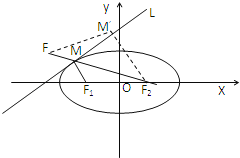
【题目】在直线上取一点,过作以为焦点的椭圆，则当最小时，椭圆的标准方程为____________________.

【答案】

【解析】

因为|MF1|+|MF2|=2a，即问题转化为在直线上求一点M，使M到F1，F2的距离的和最小，求出F1关于l的对称点F，即求M到F、F2的和最小，FF2的长就是所求的最小值．

设F1（﹣3，0）关于l：x﹣y+9=0的对称点 F（x，y）

则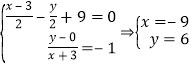，即F（﹣9，6），

连F2F交l于M，点M即为所求．

F2F：即x+2y﹣3=0

解方程组，即M（﹣5，4）

当点M′取异于M的点时，|FM′|+|M′F2|＞|FF2|．

满足题意的椭圆的长轴

所以，b2=a2﹣c2=45﹣9=36

所以椭圆的方程为：．

故答案为：

练习册系列答案
相关题目

【题目】已知抛物线y＝x2－2x及直线x＝0，x＝a，y＝0围成的平面图形的面积为，求a的值．

【题目】设函数f（x）= ，若互不相等的实数x1 ， x2 ， x3满足f（x1）=f（x2）=f（x3），则x1+x2+x3的取值范围是（ ）
A.（ ]
B.（ ）
C.（ ]
D.（ ）

【题目】已知函数f（x）在R上的导函数为f′（x），若f（x）＜2f′（x）恒成立，且f（ln4）=2，则不等式f（x）＞e 的解集是（ ）
A.（ln2，+∞）
B.（2ln2，+∞）
C.（﹣∞，ln2）
D.（﹣∞，2ln2）

【题目】在平面直角坐标系xOy中，已知圆x2+y2﹣12x+32=0的圆心为Q，过点P（0，2）且斜率为k的直线与圆Q相交于不同的两点A，B．
（1）求k的取值范围；
（2）是否存在常数k，使得向量 与 共线？如果存在，求k值；如果不存在，请说明理由．

【题目】已知函数f（x）=2cos（ωx﹣φ）（ω＞0，φ∈[0，π]）的部分图象如图所示，若A（ ， ），B（ ， ）．则下列说法错误的是（ ）

A.φ=
B.函数f（x）的一条对称轴为x=
C.为了得到函数y=f（x）的图象，只需将函数y=2sin2x的图象向右平移 个单位
D.函数f（x）的一个单调减区间为[ ， ]

【题目】已知圆C：x2＋y2＝9，点A(－5，0)，直线l：x－2y＝0.

(1)求与圆C相切，且与直线l垂直的直线方程；

(2)在直线OA上(O为坐标原点)，存在定点B(不同于点A)，满足：对于圆C上任一点P，都有为一常数，试求所有满足条件的点B的坐标．

【题目】设函数f（x）= （x＞0），观察：
f1（x）=f（x）= ，
f2（x）=f（f1（x））= ；
f3（x）=f（f2（x））= ．
f4（x）=f（f3（x））=
…
根据以上事实，当n∈N*时，由归纳推理可得：fn（1）= ．

【题目】在路边安装路灯,灯柱的高为米，路宽为23米，灯杆与灯柱角，路灯采用锥形灯罩，灯罩轴线与灯杆垂直，请你建立适当直角坐标系，解决以下问题:

(1)当

（2）且灯罩轴线正好通过道路路面的中线时，求灯杆的长为多少米？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网