题目内容
已知函数f(x)=lnx-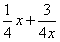 -1,
-1,
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设g(x)=-x2+2bx-4,若对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,求实数b的取值范围。
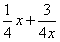 -1,
-1,(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设g(x)=-x2+2bx-4,若对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,求实数b的取值范围。
解:(Ⅰ)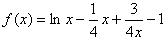 的定义域是(0,+∞),
的定义域是(0,+∞),
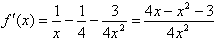 ,
,
由x>0及 ;
;
由 ,
,
故函数f(x)的单调递增区间是(1,3);单调递减区间是(0,1),(3,+∞)。
(Ⅱ)若对任意 ,不等式f(x1)≥g(x2)恒成立,
,不等式f(x1)≥g(x2)恒成立,
问题等价于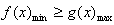 ,
,
由(Ⅰ)可知,在(0,2)上,x=1是函数极小值点,
这个极小值是唯一的极值点,故也是最小值点,
所以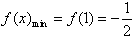 ;
;
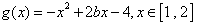 ,
,
当b<1时,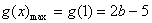 ;
;
当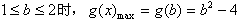 ;
;
当b>2时,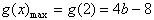 ;
;
问题等价于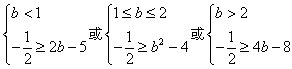 ,
,
解得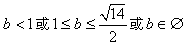 ,
,
即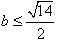 ,
,
所以实数b的取值范围是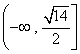 。
。
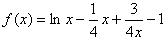 的定义域是(0,+∞),
的定义域是(0,+∞),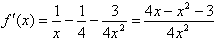 ,
,由x>0及
 ;
;由
 ,
,故函数f(x)的单调递增区间是(1,3);单调递减区间是(0,1),(3,+∞)。
(Ⅱ)若对任意
 ,不等式f(x1)≥g(x2)恒成立,
,不等式f(x1)≥g(x2)恒成立,问题等价于
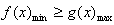 ,
,由(Ⅰ)可知,在(0,2)上,x=1是函数极小值点,
这个极小值是唯一的极值点,故也是最小值点,
所以
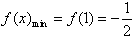 ;
;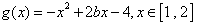 ,
,当b<1时,
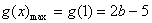 ;
;当
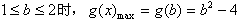 ;
;当b>2时,
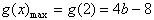 ;
;问题等价于
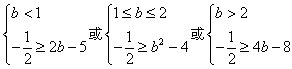 ,
,解得
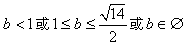 ,
,即
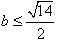 ,
,所以实数b的取值范围是
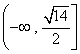 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目