题目内容
已知数列{an}满足:a1=3,an+1=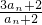 ,n∈N*,记bn=
,n∈N*,记bn=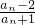 .
.
(I) 求证:数列{bn}是等比数列;
(II) 若an≤t•4n对任意n∈N*恒成立,求t的取值范围;
(III)记Cn= ,求证:C1•C2…Cn>
,求证:C1•C2…Cn> .
.
解:(Ⅰ)证明:由an+1=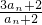 ,n∈N*得an+1-2=
,n∈N*得an+1-2=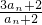 -2=
-2=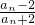 ①an+1+1=
①an+1+1=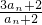 +1=
+1=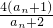 ②
②
①÷② 即bn+1=
即bn+1= bn,且
bn,且
∴数列{bn}是首项为 ,公比为
,公比为 的等比数列.(3分)
的等比数列.(3分)
(Ⅱ)由(Ⅰ)可知 ,∴
,∴
由an≤t•4n得 易得
易得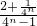 是关于n的减函数,∴
是关于n的减函数,∴ ,∴
,∴ (8分)
(8分)
(Ⅲ)由 得
得
∴C1•C2…Cn= (10分)
(10分)
下面用数学归纳法证明不等式:
若x1,x2,…xn为正数,则(1-x1)…(1-xn)>1-(x1+x2+…+xn)(*)
1°当n=2时,∵x1,x2为正数,∴(1-x1)(1-x2)=1-(x1+x2)+x1x2>1-(x1+x2)
2°假设当n=k(k≥2)时,不等式成立,即若x1,x2,…,xk为正数,则
(1-x1)(1-x2)…(1-xk)>1-(x1+x2…+xk)
那么(1-x1)(1-x2)…(1-xk)(1-xk+1)>1-(x1+x2…+xk+xk+1)
这就是说当n=k+1时不等式成立.(12分)
根据不等式(*)得:C1•C2…Cn=

∴C1•C2…Cn> .(14分)
.(14分)
分析:(Ⅰ)由条件先得 ,再分别表示∴an+1-2,an+1+1,两式相除,可得数列{bn}是首项为
,再分别表示∴an+1-2,an+1+1,两式相除,可得数列{bn}是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
(II) 由(Ⅰ)可知 ,对an≤t•4n分离参数得
,对an≤t•4n分离参数得 ,从而可解;
,从而可解;
(III)由题意可得C1•C2…Cn= ,欲证此结论,先证明:若x1,x2,…xn为正数,则(1-x1)…(1-xn)>1-(x1+x2+…+xn)成立.
,欲证此结论,先证明:若x1,x2,…xn为正数,则(1-x1)…(1-xn)>1-(x1+x2+…+xn)成立.
点评:本题考查构造新数列是求数列的通项,考查分离参数法求解恒成立问题,考查数学归纳法证明不等式,属于中档题.
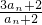 ,n∈N*得an+1-2=
,n∈N*得an+1-2=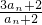 -2=
-2=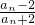 ①an+1+1=
①an+1+1=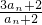 +1=
+1=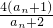 ②
②①÷②
 即bn+1=
即bn+1= bn,且
bn,且
∴数列{bn}是首项为
 ,公比为
,公比为 的等比数列.(3分)
的等比数列.(3分)(Ⅱ)由(Ⅰ)可知
 ,∴
,∴
由an≤t•4n得
 易得
易得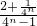 是关于n的减函数,∴
是关于n的减函数,∴ ,∴
,∴ (8分)
(8分)(Ⅲ)由
 得
得
∴C1•C2…Cn=
 (10分)
(10分)下面用数学归纳法证明不等式:
若x1,x2,…xn为正数,则(1-x1)…(1-xn)>1-(x1+x2+…+xn)(*)
1°当n=2时,∵x1,x2为正数,∴(1-x1)(1-x2)=1-(x1+x2)+x1x2>1-(x1+x2)
2°假设当n=k(k≥2)时,不等式成立,即若x1,x2,…,xk为正数,则
(1-x1)(1-x2)…(1-xk)>1-(x1+x2…+xk)
那么(1-x1)(1-x2)…(1-xk)(1-xk+1)>1-(x1+x2…+xk+xk+1)
这就是说当n=k+1时不等式成立.(12分)
根据不等式(*)得:C1•C2…Cn=


∴C1•C2…Cn>
 .(14分)
.(14分)分析:(Ⅰ)由条件先得
 ,再分别表示∴an+1-2,an+1+1,两式相除,可得数列{bn}是首项为
,再分别表示∴an+1-2,an+1+1,两式相除,可得数列{bn}是首项为 ,公比为
,公比为 的等比数列.
的等比数列.(II) 由(Ⅰ)可知
 ,对an≤t•4n分离参数得
,对an≤t•4n分离参数得 ,从而可解;
,从而可解;(III)由题意可得C1•C2…Cn=
 ,欲证此结论,先证明:若x1,x2,…xn为正数,则(1-x1)…(1-xn)>1-(x1+x2+…+xn)成立.
,欲证此结论,先证明:若x1,x2,…xn为正数,则(1-x1)…(1-xn)>1-(x1+x2+…+xn)成立.点评:本题考查构造新数列是求数列的通项,考查分离参数法求解恒成立问题,考查数学归纳法证明不等式,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目