题目内容
已知函数![]() ,且f(1)=3,
,且f(1)=3,
(1)试求a的值;
(2)用定义证明函数f(x)在[![]() ,+∞)上单调递增;
,+∞)上单调递增;
(3)设关于x的方程f(x)=x+b的两根为x1,x2,试问是否存在实数t,使得不等式![]() 对任意的b∈[2,
对任意的b∈[2,![]() ]及
]及![]() 恒成立?若存在,求出t的取值范围;若不存在说明理由.
恒成立?若存在,求出t的取值范围;若不存在说明理由.
答案:
解析:
解析:
|
解:(1)∵f(1)=3,∴a=1,∴ (2)∵a=1,∴ ∴f(x2)-f(x1)=2x2+ ∵x2>x1≥ ∴f(x2)-f(x1)>0,∴f(x2)>f(x1),∴f(x)在 (3)∵f(x)=x+b,∴x2-bx+1=0,∴|x1-x2|= 又2≤b≤ ∴令 ∴ 故 |

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 上单调递增,同理可得
上单调递增,同理可得 上单调递减.
上单调递减.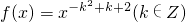 ,且f(2)<f(3)
,且f(2)<f(3)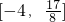 .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由. ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由. ,且f(1)=log162,f(-2)=1.
,且f(1)=log162,f(-2)=1. ,且f(1)=3。
,且f(1)=3。