题目内容
 设椭圆
设椭圆 (a>b>0)的焦点分别为F1(-1,0)、F2(1,0),直线l:x=a2交x轴于点A,且
(a>b>0)的焦点分别为F1(-1,0)、F2(1,0),直线l:x=a2交x轴于点A,且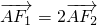 .
.
(1)试求椭圆的方程;
(2)过F1、F2分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形DMEN面积的最大值和最小值.
 解:(1)由题意,|F1F2|=2c=2,A(a2,0)
解:(1)由题意,|F1F2|=2c=2,A(a2,0)∵
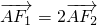
∴F2为AF1的中点
∴a2=3,b2=2
∴椭圆方程为
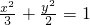 …(5分)
…(5分) (2)当直线DE与x轴垂直时,|DE|=
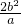 =
= ,此时|MN|=2a=2
,此时|MN|=2a=2 ,四边形DMEN的面积
,四边形DMEN的面积 .
.同理当MN与x轴垂直时,四边形DMEN的面积
 .
.当直线DE,MN均与x轴不垂直时,设DE:y=k(x+1),代入椭圆方程,消去y得:(2+3k2)x2+6k2x+(3k2-6)=0
设D(x1,y1),E(x2,y2),则x1+x2=
 ,x1x2=
,x1x2=
所以,|x1-x2|=
 ,所以|DE|=
,所以|DE|=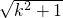 |x1-x2|=
|x1-x2|=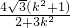 ,
,同理|MN|=
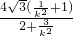 …(9分)
…(9分)所以四边形的面积
 =
= ×
×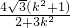 ×
×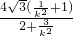 =
=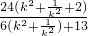
令u=
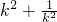 ,则S=4-
,则S=4-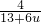
因为u=
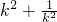 ≥2,当k=±1时,u=2,S=
≥2,当k=±1时,u=2,S= ,且S是以u为自变量的增函数,所以
,且S是以u为自变量的增函数,所以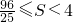 .
.综上可知,
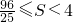 .
.故四边形DMEN面积的最大值为4,最小值为
 .…(13分)
.…(13分)分析:(1)由题意,|F1F2|=2c=2,A(a2,0),利用
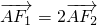 ,可得F2为AF1的中点,从而可得椭圆方程;
,可得F2为AF1的中点,从而可得椭圆方程;(2)分类讨论:当直线DE(或MN)与x轴垂直时,四边形DMEN的面积
 ;当直线DE,MN均与x轴不垂直时,设DE:y=k(x+1),代入消去y,求出|DE|,|MN|,从而可得四边形的面积的表达式,利用换元法,即可求得结论.
;当直线DE,MN均与x轴不垂直时,设DE:y=k(x+1),代入消去y,求出|DE|,|MN|,从而可得四边形的面积的表达式,利用换元法,即可求得结论.点评:本题考查椭圆的标准方程,考查四边形面积的计算,考查分类讨论的数学思想,考查韦达定理的运用,正确求弦长是关键.

练习册系列答案
相关题目













 (“a>b〉0)的左焦点为
(“a>b〉0)的左焦点为 ,椭圆过点P(
,椭圆过点P( )
) 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围. +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.