题目内容
函数f(x)=2cos(ωx+φ)( ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且|AB|=4 ,则函数f(x)图象的一条对称轴的方程为
,则函数f(x)图象的一条对称轴的方程为
A.x=2 B.x=2π C.x= D.x=
D.x=

 ,则函数f(x)图象的一条对称轴的方程为
,则函数f(x)图象的一条对称轴的方程为A.x=2 B.x=2π C.x=
 D.x=
D.x=

A
因为 ,函数最大和最小值之差为4,所以
,函数最大和最小值之差为4,所以 两点之间横坐标差值为4,则函数的最小正周期为8,故
两点之间横坐标差值为4,则函数的最小正周期为8,故 。因为函数
。因为函数 是奇函数,所以
是奇函数,所以 。而
。而 ,所以
,所以 ,故可得
,故可得 。令
。令 可得函数图象的对称轴方程为
可得函数图象的对称轴方程为 。当
。当 时可得
时可得 , 故选A。
, 故选A。
 ,函数最大和最小值之差为4,所以
,函数最大和最小值之差为4,所以 两点之间横坐标差值为4,则函数的最小正周期为8,故
两点之间横坐标差值为4,则函数的最小正周期为8,故 。因为函数
。因为函数 是奇函数,所以
是奇函数,所以 。而
。而 ,所以
,所以 ,故可得
,故可得 。令
。令 可得函数图象的对称轴方程为
可得函数图象的对称轴方程为 。当
。当 时可得
时可得 , 故选A。
, 故选A。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
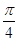 )cos(
)cos(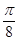
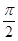
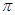
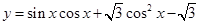 的图象的一条对称轴是( )
的图象的一条对称轴是( )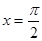
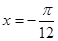
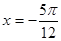
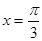

 的最小值及此时x的取值集合;
的最小值及此时x的取值集合; 个单位后所得图象关于y轴对称,求m的最小值。
个单位后所得图象关于y轴对称,求m的最小值。 。
。
 的最小值和最小正周期;
的最小值和最小正周期; 内角A、B、C的对边分别为a、b、c,满足
内角A、B、C的对边分别为a、b、c,满足 且
且 ,求a、b的值。
,求a、b的值。 ,若
,若 ,则x的取值范围为
,则x的取值范围为



 ,则
,则 的最大值为
的最大值为  ,求
,求 的值
的值