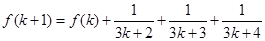题目内容
下面四个判断中,正确的是
- A.f(k)=1+k+k2+…+kn(n∈N*),当n=1时,f(k)恒为1
- B.f(k)=1+k+k2+…+kn-1(n∈N*),当n=1时,f(k)恒为1+k
- C.f(n)=1+
 +
+ +…+
+…+ (n∈N*),当n=1时,f(n)为1+
(n∈N*),当n=1时,f(n)为1+ +
+
- D.f(n)=
 +
+ +…+
+…+ (n∈N*),则f(k+1)=f(k)+
(n∈N*),则f(k+1)=f(k)+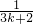 +
+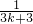 +
+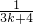
A
分析:f(k)即当n=1时,1+k+k2+…+kn的值,其实它只有一项,对于f(n)=1+ +
+ +…+(n∈N*)而言,它也只有一项.
+…+(n∈N*)而言,它也只有一项.
注意当n从k到k+1时变化的项,包括增加和减少的项.
解答:对于A,f(1)恒为1,正确;
对于B,f(1)恒为1,错误;
对于C,f(1)恒为1,错误;
对于D,f(k+1)=f(k)+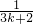 +
+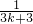 +
+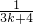 -
- ,错误;
,错误;
故选A.
点评:本题主要考查数学归纳法,数学归纳法的基本形式:P(n0)和(k)到P(k+1)的变化情况.
分析:f(k)即当n=1时,1+k+k2+…+kn的值,其实它只有一项,对于f(n)=1+
 +
+ +…+(n∈N*)而言,它也只有一项.
+…+(n∈N*)而言,它也只有一项.注意当n从k到k+1时变化的项,包括增加和减少的项.
解答:对于A,f(1)恒为1,正确;
对于B,f(1)恒为1,错误;
对于C,f(1)恒为1,错误;
对于D,f(k+1)=f(k)+
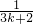 +
+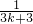 +
+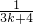 -
- ,错误;
,错误;故选A.
点评:本题主要考查数学归纳法,数学归纳法的基本形式:P(n0)和(k)到P(k+1)的变化情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下面四个判断中,正确的是( )
| A、f(k)=1+k+k2+…+kn(n∈N*),当n=1时,f(k)恒为1 | ||||||||||||
| B、f(k)=1+k+k2+…+kn-1(n∈N*),当n=1时,f(k)恒为1+k | ||||||||||||
C、f(n)=1+
| ||||||||||||
D、f(n)=
|
 ,当
,当 时为1
时为1 ,当
,当
 ,当
,当
 ,则
,则