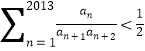题目内容
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.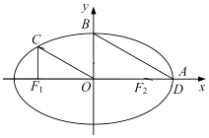
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.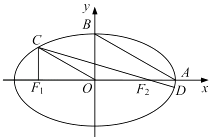
【答案】
(1)
解:椭圆 ![]() =1(a>b>0)的焦距为2c,
=1(a>b>0)的焦距为2c,
由CF1⊥x轴.则C(﹣c,y0),y0>0,
由C在椭圆上,则y0= ![]() ,则C(﹣c,
,则C(﹣c, ![]() ),
),
由OC∥AB,则﹣ ![]() =kOC=kAB=﹣
=kOC=kAB=﹣ ![]() ,则b=c,
,则b=c,
e= ![]() =
= ![]() =
= ![]() ,
,
e的值 ![]()
(2)
解:设D(x1,y1),设 ![]() =λ
=λ ![]() ,
,
C(﹣c, ![]() ),F2(c,0),
),F2(c,0),
故 ![]() =(2c,﹣
=(2c,﹣ ![]() ),
), ![]() =(x1﹣c,y1),
=(x1﹣c,y1),
由 ![]() =λ
=λ ![]() ,则2c=λ(x1﹣c),﹣
,则2c=λ(x1﹣c),﹣ ![]() =λy1,则D(
=λy1,则D( ![]() c,﹣
c,﹣ ![]() ),
),
由点D在椭圆上,则( ![]() )2e2+
)2e2+ ![]() =1,整理得:(λ2+4λ+3)e2=λ2﹣1,
=1,整理得:(λ2+4λ+3)e2=λ2﹣1,
由λ>0,e2= ![]() =
= ![]() =1﹣
=1﹣ ![]() ,
,
由 ![]() ≤e≤
≤e≤ ![]() ,则
,则 ![]() ≤e2≤
≤e2≤ ![]() ,则
,则 ![]() ≤1﹣
≤1﹣ ![]() ≤
≤ ![]() ,
,
解得: ![]() ≤λ≤5,
≤λ≤5,
∴ ![]() 的取值范围[
的取值范围[ ![]() ,5]
,5]
【解析】(1)由CF1⊥x轴.则C(﹣c, ![]() ),根据直线的斜率相等,即可求得b=c,利用离心率公式即可求得e的值;(2)根据向量的坐标运算,求得D点坐标,代入椭圆方程,求得e2=
),根据直线的斜率相等,即可求得b=c,利用离心率公式即可求得e的值;(2)根据向量的坐标运算,求得D点坐标,代入椭圆方程,求得e2= ![]() =1﹣
=1﹣ ![]() ,由离心率的取值范围,即可求得λ的取值范围.
,由离心率的取值范围,即可求得λ的取值范围.

练习册系列答案
相关题目