题目内容
(16分)设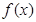 使定义在区间
使定义在区间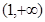 上的函数,其导函数为
上的函数,其导函数为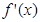 .如果存在实数
.如果存在实数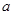 和函数
和函数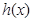 ,其中
,其中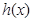 对任意的
对任意的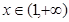 都有
都有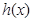 >0,使得
>0,使得 ,则称函数
,则称函数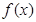 具有性质
具有性质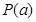 .
.
(1)设函数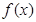
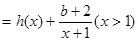 ,其中
,其中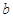 为实数
为实数
①求证:函数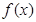 具有性质
具有性质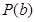
②求函数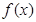 的单调区间
的单调区间
(2)已知函数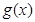 具有性质
具有性质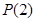 ,给定
,给定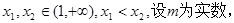
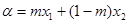 ,
,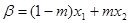 ,且
,且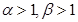 ,若|
,若|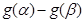 |<|
|<|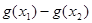 |,求
|,求 的取值范围
的取值范围
【答案】
(1)估计该问题目有错,似乎为
 ,则有如下解答:
,则有如下解答:
①

∵ 时,
时, 恒成立,
恒成立,
∴函数 具有性质
具有性质 ;
;

【解析】

练习册系列答案
相关题目
 使定义在区间
使定义在区间 上的函数,其导函数为
上的函数,其导函数为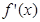 .如果存在实数
.如果存在实数 和函数
和函数 ,其中
,其中 都有
都有 ,则称函数
,则称函数 .
. ,其中
,其中 为实数
为实数
 具有性质
具有性质 ,给定
,给定
 ,
, ,且
,且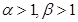 ,若|
,若| |<|
|<| |,求
|,求 的取值范围
的取值范围 使定义在区间
使定义在区间 上的函数,其导函数为
上的函数,其导函数为 .如果存在实数
.如果存在实数 和函数
和函数 ,其中
,其中 都有
都有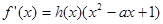 ,则称函数
,则称函数 .
. ,其中
,其中 为实数
为实数
 具有性质
具有性质 ,给定
,给定
 ,
, ,且
,且 ,若|
,若| |<|
|<| |,求
|,求 的取值范围
的取值范围 使定义在区间
使定义在区间 上的函数,其导函数为
上的函数,其导函数为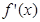 .如果存在实数
.如果存在实数 和函数
和函数 ,其中
,其中 都有
都有 ,则称函数
,则称函数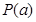 .
. ,其中
,其中 为实数
为实数
 具有性质
具有性质 ,给定
,给定
 ,
, ,且
,且 ,若|
,若| |<|
|<| |,求
|,求 的取值范围
的取值范围 使定义在区间
使定义在区间 上的函数,其导函数为
上的函数,其导函数为 .如果存在实数
.如果存在实数 和函数
和函数 ,其中
,其中 都有
都有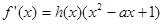 ,则称函数
,则称函数 .
. ,其中
,其中 为实数
为实数
 具有性质
具有性质 ,给定
,给定
 ,
, ,且
,且 ,若|
,若| |<|
|<| |,求
|,求 的取值范围
的取值范围 使定义在区间
使定义在区间 上的函数,其导函数为
上的函数,其导函数为 .如果存在实数
.如果存在实数 和函数
和函数 ,其中
,其中 都有
都有 ,则称函数
,则称函数 .
. ,其中
,其中 为实数
为实数
 具有性质
具有性质 ,给定
,给定
 ,
, ,且
,且 ,若|
,若| |<|
|<| |,求
|,求 的取值范围
的取值范围