题目内容
【题目】如图,四棱锥PABCD的底面为正方形,PD底面ABCD.设平面PAD与平面PBC的交线为![]() .
.
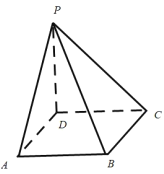
(1)证明:![]() 平面PDC;
平面PDC;
(2)已知PDAD1,Q为![]() 上的点,QB=
上的点,QB=![]() ,求PB与平面QCD所成角的正弦值.
,求PB与平面QCD所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用线面平行的判定定理以及性质定理,证得![]() ,利用线面垂直的判定定理证得
,利用线面垂直的判定定理证得![]() 平面
平面![]() ,从而得到
,从而得到![]() 平面
平面![]() ;
;
(2)根据题意,建立相应的空间直角坐标系,得到相应点的坐标,设出点![]() ,之后求得平面
,之后求得平面![]() 的法向量以及向量
的法向量以及向量![]() 的坐标,求得
的坐标,求得![]() ,即可得到直线
,即可得到直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:
在正方形![]() 中,
中,![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,
,
因为在四棱锥![]() 中,底面
中,底面![]() 是正方形,所以
是正方形,所以![]()
且![]() 平面
平面![]() ,所以
,所以![]()
因为![]()
所以![]() 平面
平面![]() ;
;
(2)如图建立空间直角坐标系![]() ,
,
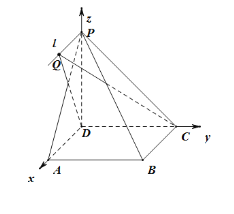
因为![]() ,则有
,则有![]() ,
,
设![]() ,则有
,则有![]() ,
,
因为QB=![]() ,所以有
,所以有![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则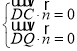 ,即
,即![]() ,
,
令![]() ,则
,则![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
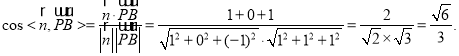
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于![]()
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
