题目内容
已知不等式m2+(sin2θ-4)m+3cos2θ≥0恒成立,则实数m的取值范围是 .
【答案】分析:本题是利用三角函数公式将抽象不等式变为三角不等式,再由三角函数的有界性结合一次函数的性质求参数m的范围.
解答:解:∵m2+(sin2θ-4)m+3cos2θ≥0,
∴m2+(sin2θ-4)m+3(1-sin2θ)≥0;
∴sin2θ(m-3)+m2-4m+3≥0恒成立
?不等式 恒成立
恒成立
?m≤0或m≥3,
故答案为m≤0或m≥3.
点评:本题考点是函数恒成立问题,本题利用函数的性质将不等式恒成立求参数的问题转化为求函数最值的问题,本题中转化后求最值要注意三角函数的有界性,求解本题时两次利用转化的思想,第一次是将不等式转化为三角不等式,第二次是将三角不等式转化为求一次函数在某个区间上的最值,解题时要注意理解、领会本题中的转化策略及理论依据.
解答:解:∵m2+(sin2θ-4)m+3cos2θ≥0,
∴m2+(sin2θ-4)m+3(1-sin2θ)≥0;
∴sin2θ(m-3)+m2-4m+3≥0恒成立
?不等式
 恒成立
恒成立?m≤0或m≥3,
故答案为m≤0或m≥3.
点评:本题考点是函数恒成立问题,本题利用函数的性质将不等式恒成立求参数的问题转化为求函数最值的问题,本题中转化后求最值要注意三角函数的有界性,求解本题时两次利用转化的思想,第一次是将不等式转化为三角不等式,第二次是将三角不等式转化为求一次函数在某个区间上的最值,解题时要注意理解、领会本题中的转化策略及理论依据.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
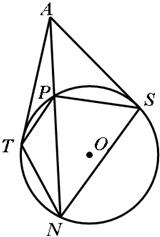 选做题A.平面几何选讲
选做题A.平面几何选讲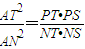 .
.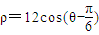 上的动点,试求线段AB长的最大值.D.不等式选讲
上的动点,试求线段AB长的最大值.D.不等式选讲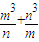 ≥m2+n2.
≥m2+n2.