题目内容
若对一切正数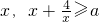 都成立,则a的最大值为
都成立,则a的最大值为
- A.2
- B.3
- C.

- D.4
D
分析:要使对一切正数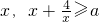 都成立只需
都成立只需 的最小值大于等于a,即a小于等于
的最小值大于等于a,即a小于等于 的最小值,由基本不等式可得
的最小值,由基本不等式可得 的最小值.
的最小值.
解答:设y= ,x>0
,x>0
由基本不等式可得:设y=

当且仅当x= ,即x=2时取到等号,ymin=4
,即x=2时取到等号,ymin=4
对一切正数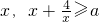 都成立等价于ymin≥a,
都成立等价于ymin≥a,
即a≤4,故a的最大值为:4
故选D.
点评:本题为求最大值问题,利用基本不等式求得 的最小值是解决问题的关键,属基础题.
的最小值是解决问题的关键,属基础题.
分析:要使对一切正数
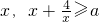 都成立只需
都成立只需 的最小值大于等于a,即a小于等于
的最小值大于等于a,即a小于等于 的最小值,由基本不等式可得
的最小值,由基本不等式可得 的最小值.
的最小值.解答:设y=
 ,x>0
,x>0由基本不等式可得:设y=


当且仅当x=
 ,即x=2时取到等号,ymin=4
,即x=2时取到等号,ymin=4对一切正数
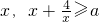 都成立等价于ymin≥a,
都成立等价于ymin≥a,即a≤4,故a的最大值为:4
故选D.
点评:本题为求最大值问题,利用基本不等式求得
 的最小值是解决问题的关键,属基础题.
的最小值是解决问题的关键,属基础题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
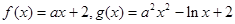 ,其中
,其中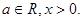
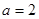 ,求曲线
,求曲线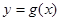 在点
在点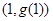 处的切线方程;
处的切线方程;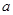 ,使
,使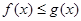 对一切正数
对一切正数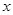 都成立?若存在,求出
都成立?若存在,求出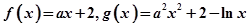 ,其中
,其中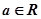 ,
,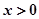 。
。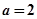 ,求曲线
,求曲线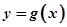 在
在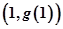 点处的切线方程;
点处的切线方程;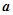 ,使
,使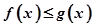 对一切正数
对一切正数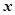 都成立?若存在,求出
都成立?若存在,求出 ,其中
,其中 ,
, 。
。 ,求曲线
,求曲线 在
在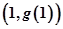 点处的切线方程;
点处的切线方程; ,使
,使 对一切正数
对一切正数 都成立?若存在,求出
都成立?若存在,求出 ,其中
,其中 ,
, 。
。 ,求曲线
,求曲线 在
在 点处的切线方程;
点处的切线方程; ,使
,使 对一切正数
对一切正数 都成立?若存在,求出
都成立?若存在,求出