题目内容
已知点A（1，1），B（1，-1），C（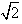
cosθ，
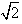sinθ）（θ∈R），O为坐标原点，
（1）若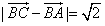
，求sin2θ的值；
（2）若实数m，n满足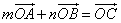
，求（m-3）2+n2的最大值。
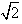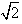cosθ，sinθ）（θ∈R），O为坐标原点，（1）若
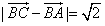，求sin2θ的值；（2）若实数m，n满足
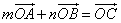，求（m-3）2+n2的最大值。 解：（1）∵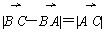
，
∴
，
∴-2
（sinθ+cosθ）+4=2，即sinθ+cosθ=
，
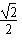两边平方得1+sin2θ=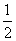
，
∴sin2θ=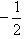
；
（2）由已知得：（m，m）+（n，-n）=（
cosθ，
sinθ），
∴
，
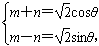解得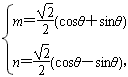
，
∴（m-3）2+n2=m2+n2-6m+9
=-3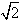
（sinθ+cosθ）+10 =-6sin（θ+
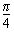）+10，
∴当sin（θ+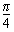
）=-1时，（m-3）2+n2取得最大值16。
，∴
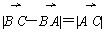，∴-2
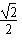（sinθ+cosθ）+4=2，即sinθ+cosθ=，两边平方得1+sin2θ=
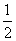， ∴sin2θ=
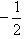；（2）由已知得：（m，m）+（n，-n）=（
cosθ，sinθ）， ∴
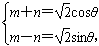，解得
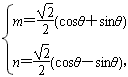，∴（m-3）2+n2=m2+n2-6m+9
=-3
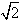（sinθ+cosθ）+10 =-6sin（θ+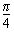）+10，∴当sin（θ+
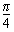）=-1时，（m-3）2+n2取得最大值16。 
练习册系列答案
相关题目
在平面直角坐标系xoy中，已知点A（-1，1），P是动点，且△POA的三边所在直线的斜率满足kOP+kOA=kPA